题目内容
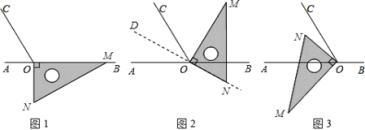
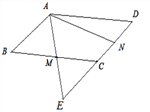
【题目】请仔细观察如图所示的折纸过程,然后回答下列问题:

(1)![]() 的度数为__________;
的度数为__________;
(2)![]() 与
与![]() 有何数量关系:______;
有何数量关系:______;
(3)![]() 与
与![]() 有何数量关系:__________;
有何数量关系:__________;
【答案】(1)90°;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由图中第三个图形可知,折叠后∠1+∠3=∠2,再根据B、E、C三点共线可求得结论;
(2)根据(1)可知∠1+∠3=∠2=90°,两角之和为90°,两角互余;
(3)由B、E、C三点共线可得出结论.
解:(1)根据折叠的过程可知:∠2=∠1+∠3,
∵∠1+∠2+∠3=∠BEC,B、E、C三点共线
∴∠2=180°÷2=90°.
故答案是:90°.
(2)∵∠1+∠3=∠2,
∴∠1+∠3=90°.
故答案是:∠1+∠3=90°.
(3)∵B、E、C三点共线,
∴∠1+∠AEC=180°,
故答案是:∠1+∠AEC=180°.

练习册系列答案
相关题目
【题目】在一次社会调查活动中,小李收集到某“健步走运动”团队20名成员一天行走的步数,记录如下:
5640 | 6430 | 6520 | 6798 | 7325 |
8430 | 8215 | 7453 | 7446 | 6754 |
7638 | 6834 | 7326 | 6830 | 8648 |
8753 | 9450 | 9865 | 7290 | 7850 |
对这20个数据按组距1000进行分组,并统计整理.

(1)请完成下面频数分布统计表;
组别 | 步数分组 | 频数 |
A | 5500≤x<6500 | |
B | 6500≤x<7500 | |
C | 7500≤x<8500 | |
D | 8500≤x<9500 | |
E | 9500≤x<10500 |
(2)在上图中请画出频数分布直方图;
(3)若该团队共有200人,请估计其中一天行走步数少于8500步的人数.