题目内容
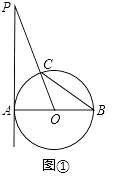
【题目】如图,AB是⊙O的直径,PA切⊙O于A,OP交⊙O于C,连接BC.
(Ⅰ)如图①,若∠P=20°,求∠BCO的度数;
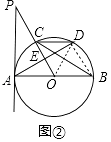
(Ⅱ)如图②,过A作弦AD⊥OP于E,连接DC,若OE= ![]() CD,求∠P的度数.
CD,求∠P的度数.
【答案】解:(Ⅰ)如图1中,
∵PA是⊙O的切线,
∴OA⊥AP,
∴∠PAO=90°,∵∠P=20°,
∴∠AOC=90°﹣20°=70°,
∴∠B= ![]() ∠AOC=35°,
∠AOC=35°,
∵OB=OC,
∴∠B=∠OCB=35°,
∴∠BCO=35°.
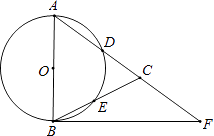
(Ⅱ)如图2中,连接BD、OD.
∵AD⊥OP于E,
∴AE=ED, ![]() =
= ![]() ,
,
∵AE=ED,OA=OB,
∴OE= ![]() DB,
DB,
∵OE= ![]() CD,
CD,
∴CD=DB,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴∠AOC=∠COD=∠BOD=60°,
∵PA是⊙O的切线,
∴∠PAO=90°,
∴∠P=30°
【解析】(1)可利用切线的性质得出垂直,再利用等边对等角的性质求出答案;(2)可利用直径的性质须连接BD,构成90度的圆周角,再利用垂径定理及其推论可求出∠P=30°.
【考点精析】解答此题的关键在于理解垂径定理的相关知识,掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,以及对切线的性质定理的理解,了解切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

练习册系列答案
相关题目