题目内容
【题目】已知直线l:y=kx和抛物线C:y=ax2+bx+1.
(Ⅰ)当k=1,b=1时,抛物线C:y=ax2+bx+1的顶点在直线l:y=kx上,求a的值;
(Ⅱ)若把直线l向上平移k2+1个单位长度得到直线r,则无论非零实数k取何值,直线r与抛物线C都只有一个交点;
(i)求此抛物线的解析式;
(ii)若P是此抛物线上任一点,过点P作PQ∥y轴且与直线y=2交于点Q,O为原点,求证:OP=PQ.
【答案】解:(Ⅰ)将k=1,b=1代入代入得:抛物线的解析式为y=ax2+x+1,直线的解析式为y=x.
∵y=ax2+x+1=a(x+ ![]() )2+1﹣
)2+1﹣ ![]() ,
,
∴抛物线的顶点为(﹣ ![]() ,1﹣
,1﹣ ![]() ).
).
∵抛物线的顶点在直线y=x上,
∴﹣ ![]() =1﹣
=1﹣ ![]() ,解得:a=﹣
,解得:a=﹣ ![]() .
.
(Ⅱ)(i)将直线y=kx向上平移k2+1个单位,所得直线的解析式为y=kx+k2+1.
∵无论非零实数k取何值,直线与抛物线都只有一个交点,
∴方程kx+k2+1=ax2+bx+1有两个相等的实数根,即ax2+(b﹣k)x﹣k2=0有两个相等的实数根,
∴△=(b﹣k)2+4ak2=(4a+1)k2﹣2bk+b2=0.
∵无论非零实数k取何值时,(4a+1)k2﹣2bk+b2=0恒成立,
∴4a+1=0且b=0,
∴a=﹣ ![]() ,b=0.
,b=0.
∴抛物线的解析式为y=﹣ ![]() x2+1.
x2+1.
(ii)证明:根据题意,画出图象如图所示:
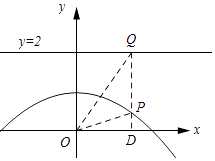
设点P的坐标为(x,﹣ ![]() x2+1)则点Q的坐标为(x,2),D(x,0).
x2+1)则点Q的坐标为(x,2),D(x,0).
∴PD=|﹣ ![]() x2+1|,OD=|x|,QP=2﹣(﹣
x2+1|,OD=|x|,QP=2﹣(﹣ ![]() x2+1)=
x2+1)= ![]() x2+1.
x2+1.
在Rt△OPD中,依据勾股定理得:OP= ![]() =
= ![]() =
= ![]() x2+1.
x2+1.
∴OP=PQ
【解析】(1)利用配方法求出顶点坐标,代入y=x中即可;(2)可联立直线和抛物线解析式得到的方程判别式恒等于0,可得出a、b的值;(3)可表示出OP,PQ,证得二者相等.
【考点精析】本题主要考查了二次函数的图象的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点才能正确解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案