题目内容
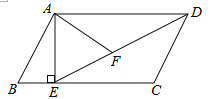
【题目】在平面直角坐标系中,过一点分別作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则称这个点为强点.例如,图中过点P分別作x轴,y轴的垂线与坐标轴围成矩形OAPB的周长与面积相等,则点P是强点.
(1)点M(l,2),N(4,4),Q(6,-3)中,是强点的有 ;
(2)若强点P(2a,3)在双曲线![]() 上,求a和b的值.
上,求a和b的值.

【答案】(1)N,Q;(2)a=3,b=20或a=3,b=16
【解析】
(1)利用矩形的周长公式、面积公式结合强点的定义,即可找出点N,Q是强点;
(2)分a>0及a<0两种情况考虑:①当a>0时,利用强点的定义可得出关于a的一元一次方程,解之可得出a的值,再利用反比例函数图象上点的坐标特征可求出b值;②当a<0时,利用强点的定义可得出关于a的一元一次方程,解之可得出a的值,再利用反比例函数图象上点的坐标特征可求出b值.综上,即可得出结论.
(1)∵M(l,2),N(4,4),Q(6,-3)
∵(1+2)×2≠1×2,(4+4)×2=4×4,(6+3)×2=6×3,
∴点N,Q是强点.
故答案为:N,Q
(2)分两种情况考虑:
①当a>0时,(2a+3)×2=6a,
∴a=3
∵点P(6,3)在双曲线![]() 上,
上,
∴3×6= b-2,
∴b=20;
②当a<0时,(2a+3)×2=6a,
∴a=3
∵点P(6,3)在双曲线![]() 上,
上,
∴3×(-6)=b-2,
∴b=16
综上所述:a=3,b=20或a=3,b=16
故答案为:a=3,b=20或a=3,b=16

 名校课堂系列答案
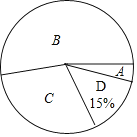
名校课堂系列答案【题目】某市将开展以“走进中国数学史”为主题的知识凳赛活动,红树林学校对本校100名参加选拔赛的同学的成绩按A,B,C,D四个等级进行统计,绘制成如下不完整的统计表和扇形统计图:
成绩等级 | 频数(人数) | 频率 |
A | 4 | 0.04 |
B | m | 0.51 |
C | n | |
D | ||
合计 | 100 | 1 |
(1)求m= ,n= ;
(2)在扇形统计图中,求“C等级”所对应心角的度数;
(3)成绩等级为A的4名同学中有1名男生和3名女生,现从中随机挑选2名同学代表学校参加全市比赛,请用树状图法或者列表法求出恰好选中“1男1女”的概率.
【题目】某市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了四次测试,测试成绩如表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | |
甲 | 9 | 8 | 8 | 7 |
乙 | 10 | 6 | 7 | 9 |
(1)根据表格中的数据,分别计算甲、乙两名运动员的平均成绩;
(2)分别计算甲、乙两人四次测试成绩的方差;根据计算的结果,你认为推荐谁参加省比赛更合适?请说明理由.
【题目】我市某校组织“学经典,用经典”知识竞赛,每班参加比赛的学生人数相同,成绩分为![]() 四个等级,其中相应等级的得分依次记为
四个等级,其中相应等级的得分依次记为![]() 分,
分,![]() 分,
分,![]() 分,
分,![]() 分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:
分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:
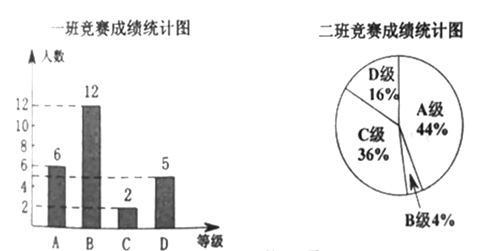
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩“![]() 级”的人数为 ;
级”的人数为 ;
(2)请你将下表补充完整:
平均数(分) | 中位数(分) | 众数(分) | |
一班 |
|
| |
二班 |
|
|
(3)请你对这次两班成绩统计数据的结果进行分析(写出一条结论即可)