题目内容
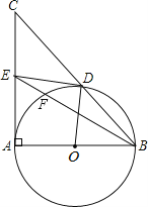
【题目】 如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交弧AC于点D,过点D作⊙O的切线,交BA的延长线于点E,连接CD,OC.
(1)求证:AC∥DE;
(2)若OA=AE,求证:△AFO≌△CFD;
(3)若OA=AE=2,则四边形ACDE的面积是______.

【答案】(1)详见解析;(2)详见解析;(3)2![]() .
.
【解析】
(1)先根据切线的性质得出OD⊥DE,再根据垂定定理得出OD⊥AC,即可得出结论;
(2)先判断出OE=2OD,进而得出∠E=30°,进而得出∠C=30°=∠OAF,即可用ASA判断出△AFO≌△CFD;
(3)先求出△ODE的面积,再根据(2)△AFO≌△CFD,得出S△AFO=S△CFD,即可得出结论.
(1)证明:∵DE是⊙O的切线,
∴OD⊥DE,
∵F为⊙O中弦AC的中点,
∴OD⊥AC,
∴AC∥DE;
(2)解:如图,
连接CD,由(1)知,OD⊥DE,
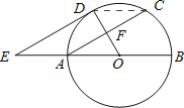
∴∠ODE=90°,
∵OA=AE,
∴OE=AE+OA=2OA,
∵OA=OD,
∴OE=2OD,
在Rt△ODE中,OE=2OD,
∴∠E=30°,
∴∠DOE=90°-30°=60°,
∴∠C=![]() ∠AOD=30°,
∠AOD=30°,
由(1)知,AC∥DE,
∴∠OAF=∠E=30°=∠C,
∵点F是AC的中点,
∴AF=CF,
由(1)知,OD⊥AC,
∴∠AFO=∠CFD=90°,
在△AFO和△CFD中,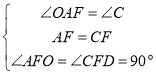
∴△AFO≌△CFD(ASA);
(3)∵OA=AE=2,
∴OE=OA+AE=4,OD=OA=2,
根据勾股定理得,DE=![]() =
=![]() =2
=2![]() ,
,
∴S△ODE=![]() ODDE=
ODDE=![]() ×2×2
×2×2![]() =2
=2![]()
由(2)知,△AFO≌△CFD,
∴S△AFO=S△CFD,
∴S四边形ACDE=S四边形DEAF+S△CFD=S四边形DEAF+S△AFO=S△ODE=2![]() ,
,
故答案为:2![]() .
.