Question

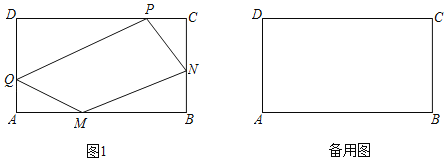
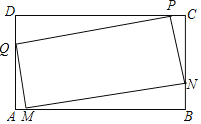
【题目】如图1，点M，N，P，Q分别在矩形ABCD的边AB，BC，CD，DA上，我们称四边形MNPQ是矩形ABCD的内接四边形．已知矩形ABCD，AB＝2BC＝6，若它的内接四边形MNPQ也是矩形，且相邻两边的比为3：1，则AM＝_____．

Answer 1

【答案】

【解析】

证明△AMQ∽△DQP，△PCN∽△NBM，设MA＝x，则DQ＝3x，QA＝3﹣3x，DP＝9﹣9x，PC＝9x﹣3，NB＝27x﹣9，表示出NC，由BC长为3，可得方程，解方程即可得解．

解：∵四边形ABCD和四边形MNPQ为矩形，

∴∠D＝∠A＝90°，∠DQP＝∠QMA，

∴△AMQ∽△DQP，

同理△PCM∽△NBM，

设MA＝x，∵PQ：QM＝3：1，

∴DQ＝3x，QA＝3﹣3x，DP＝9﹣9x，

PC＝6﹣（9﹣9x）＝9x﹣3，NB＝3PC＝27x﹣9，

BM＝6﹣x，

∴NC＝，

∴＝3，

解得x＝．

即AM＝．

故答案为：．