��Ŀ����
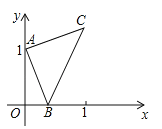
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�����y��![]() ��x��0����ͼ����ֱ��y��x��2���ڵ�A��3��m����
��x��0����ͼ����ֱ��y��x��2���ڵ�A��3��m����
��1����k��m��ֵ��
��2����֪��P��n��n����n��0��������P��ƽ����x���ֱ�ߣ���ֱ��y��x��2�ڵ�M������P��ƽ����x���ֱ�߽�����y��![]() ��x��0��x��ͼ���ڵ�N��
��x��0��x��ͼ���ڵ�N��
����n��3ʱ���ж��߶�PM��PN��������ϵ����˵�����ɣ�
����PN��PM����Ϻ�����ͼ��ֱ��д��n��ȡֵ��Χ��
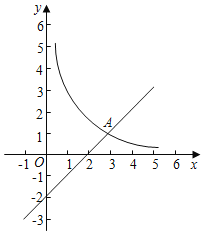
���𰸡���1��m��1�� k��3����2����PM��PN�����������������0��n��1��n��3
��������
��1����A�����y��x��2�м������m��ֵ��Ȼ��A��������뷴���������м������k��ֵ��
��2���ٵ�n��3ʱ���ֱ����M��N��������꼴�����PM��PN�Ĺ�ϵ��
�ڸ���P������Ϊ��n��n�������M�����꣬�ɵ�PM��2������PN��PM���Ӷ���֪PN��2��Ȼ�����ͼ������n�ķ�Χ��
�⣺��1����A��3��m������y��x��2����m��3��2��1��
��A��3��1����
��A��3��1������y��![]() ��
��
��k��3��1��3��
�෴���������Ľ���ʽΪ��y��![]() ��
��
��2���ٵ�n��3ʱ��P��3��3����
��y��3������y��x��2����x��2��3��
��x��5��
��M��5��3����
��PM��2��
��x��3������y��![]() ����y��1��
����y��1��
��N��3��1����
��PN��2��
��PM��PN��
����P��n��n����n��0��֪����P��ֱ��y��x�ϣ�
����P��ƽ����x���ֱ�ߣ���ֱ��y��x��2�ڵ�M����M��n+2��n����
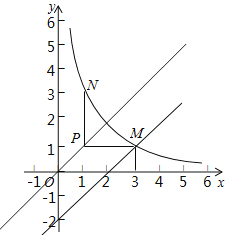
��PM��2��
��PN��PM����PN��2����PN��![]() ��
��
��![]() ��2��
��2��
��ͼ��ɵã�0��n��1��n��3.

����Ŀ�����Ż��������ƶ��ն˵�Ѹ�ٷ�չ�����ֻ��Ķ�Խ��Խ�ռ��������������ϵ�����ͷ����Խ��Խ�࣬ij�о��������������ο������ֻ��Ķ����������������ʾ����飨�ʾ����������ͼ��ʾ�����������������Ƴ�ͼ�ٺ�ͼ����ʾ��ͳ��ͼ��������������
������ο������ֻ��Ķ����ʾ������
���ã�����һ�ݹ���������ο������ֻ��Ķ��ʾ�����������ڱ�����ѡ��һ��������ͬ�Ĺ۵㣬�����ո��ڴ����̡����dz���л���ĺ�����
���� | �۵� | |
| ��ȡ��Ϣ���㣬������ʱ��عۿ� | |
| �۸������ | |
| ʹ�����dz�Ϊ����ͷ�������������˼ʽ��� | |
| ���ݷḻ����ֽ�������Ը��� | |
| ���� | |
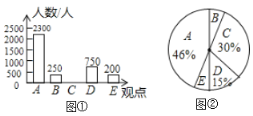
�����ͳ��ͼ���ṩ����Ϣ������������⣺
��I�����ν��ܵ������������__________�ˣ���������ͳ��ͼ����������
����������ͳ��ͼ�У��۵�![]() �İٷֱ���___________����ʾ�۵�
�İٷֱ���___________����ʾ�۵�![]() �����ε�Բ�ĽǶ���Ϊ_________�ȣ�
�����ε�Բ�ĽǶ���Ϊ_________�ȣ�
����ij�й���![]() ���ˣ���������ϵ�����������г�
���ˣ���������ϵ�����������г�![]() ��
��![]() ��
��![]() �۵������ֻ��Ķ����������ж������ˣ�
�۵������ֻ��Ķ����������ж������ˣ�