题目内容
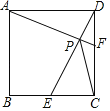
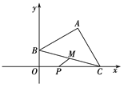
【题目】在平面直角坐标系中,点C、B分别在![]() 轴、
轴、![]() 轴上,△ABC是等腰直角三角形,∠BAC=90°,已知A(2,2)、P(1,0).M为BC的中点,则PM的最小值为_____.
轴上,△ABC是等腰直角三角形,∠BAC=90°,已知A(2,2)、P(1,0).M为BC的中点,则PM的最小值为_____.
【答案】![]()
【解析】
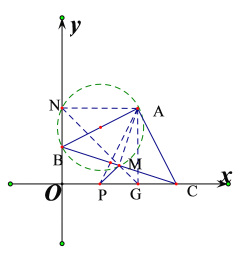
连接AM,AP,过点A作AG⊥x轴于点G,过点A作AN⊥y轴于点N,连接MN,易得四边形AGON是正方形,由∠AMB=∠ANO =90°,可得点A,N,B,M四点共圆,进而得点M是正方形的对角线NG上的一个动点,当PM⊥NG时,PM的值最小,此时,PMG是等腰直角三角形,进而即可得到答案.
连接AM,AP,过点A作AG⊥x轴于点G,过点A作AN⊥y轴于点N,连接MN,
∵A(2,2),
∴AN=AG=2,∠ANO=∠AGO=∠NOG=90°,
∴四边形AGON是正方形,
∵△ABC是等腰直角三角形,∠BAC=90°,M为BC的中点,
∴∠ABC=45°,∠AMB=90°,
∴点A,N,B,M四点共圆,
∴∠ANM=∠ABC=45°,
∴点M是正方形的对角线NG上的一个动点,
∴当PM⊥NG时,PM的值最小,此时,PMG是等腰直角三角形,
∵P(1,0),OG=2,
∴PG=1,
∴PM的最小值=PG÷![]() =1÷
=1÷![]() =
=![]() .
.
故答案是:![]() .
.

【题目】洛阳某科技公司生产和销售A、B两类套装电子产品![]() 已知3套A类产品和2套B类产品的总售价是24万元;2套A类产品和3套B类产品的总售价是26万元
已知3套A类产品和2套B类产品的总售价是24万元;2套A类产品和3套B类产品的总售价是26万元![]() 公司生产一套A类产品的成品是
公司生产一套A类产品的成品是![]() 万元,生产B类产品的成本如下表:
万元,生产B类产品的成本如下表:
套数 | 1 | 2 | 3 | 4 |
|
总成本 | 8 | 12 | 16 | 20 |
|
![]() 该公司A类产品和B类产品的销售单价分别是多少万元?
该公司A类产品和B类产品的销售单价分别是多少万元?
![]() ①公司为了方便生产,只安排生产一类电子产品,且销售顺利,设生产销售该类电子产品x套:公司销售x套A类产品的利润
①公司为了方便生产,只安排生产一类电子产品,且销售顺利,设生产销售该类电子产品x套:公司销售x套A类产品的利润![]() ________;公司销售x套B类产品的利润
________;公司销售x套B类产品的利润![]() ________.
________.
②怎样安排生产,才能使公司获得的利润较高?
【题目】鄂北公司以10元/千克的价格收购一批产品进行销售,为了得到日销售量y(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如表:
销售价格x(元/千克) | 10 | 15 | 20 | 25 | 30 |
日销售量y(千克) | 300 | 225 | 150 | 75 | 0 |
(1)请你根据表中的数据确定y与x之间的函数表达式;
(2)鄂北公司应该如何确定这批产品的销售价格,才能使日销售利润W1元最大?
(3)若鄂北公司每销售1千克这种产品需支出a元(a>0)的相关费用,当20≤x≤25时,鄂北公司的日获利W2元的最大值为1215元,求a的值.