题目内容
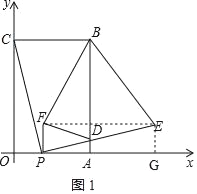
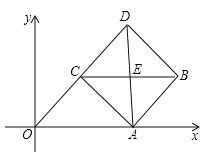
【题目】如图，在平面直角坐标系中，矩形OABC的顶点B坐标为（4，6），点P为线段OA上一动点（与点O、A不重合），连接CP，过点P作PE⊥CP交AB于点D，且PE=PC，过点P作PF⊥OP且PF=PO（点F在第一象限），连结FD、BE、BF，设OP=t．
（1）直接写出点E的坐标（用含t的代数式表示）：_____；
（2）四边形BFDE的面积记为S，当t为何值时，S有最小值，并求出最小值；
（3）△BDF能否是等腰直角三角形，若能，求出t；若不能，说明理由．
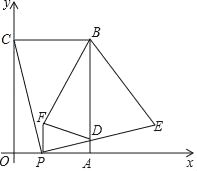
【答案】(1)、（t+6，t）；(2)、当t=2时，S有最小值是16；(3)、理由见解析．
【解析】分析：(1)、过点E作EG⊥x轴于点G，根据题意得出CO=AB=6、OA=BC=4、OP=t，然后通过角之间的关系证明△PCO和△EPG全等，从而得出答案；(2)、根据DA∥EG得出△PAD和△PGE相似，求出AD的长度，然后根据四边形的面积等于△BDF的面积加上△BDE的面积得出函数解析式，从而求出面积的最值；(3)、根据∠FBD、∠FDB、∠BFD分别为直角，证明是否存在即可得出答案．
详解：（1）如图所示，过点E作EG⊥x轴于点G，则∠COP=∠PGE=90°，
由题意知CO=AB=6、OA=BC=4、OP=t，∵PE⊥CP、PF⊥OP，
∴∠CPE=∠FPG=90°，即∠CPF+∠FPE=∠FPE+∠EPG，∴∠CPF=∠EPG，
又∵CO⊥OG、FP⊥OG，∴CO∥FP，∴∠CPF=∠PCO，∴∠PCO=∠EPG，
在△PCO和△EPG中，∵∠PCO=∠EPG，∠POC=∠EGP，PC=EP，∴△PCO≌△EPG（AAS），
∴CO=PG=6、OP=EG=t，则OG=OP+PG=6+t，则点E的坐标为（t+6，t），
（2）∵DA∥EG，∴△PAD∽△PGE，∴
，∴
，∴AD=
t（4﹣t），
∴BD=AB﹣AD=6﹣t（4﹣t）=t2﹣
t+6，∵EG⊥x轴、FP⊥x轴，且EG=FP，
∴四边形EGPF为矩形，∴EF⊥BD，EF=PG，
∴S四边形BEDF=S△BDF+S△BDE=
×BD×EF=×（t2﹣t+6）×6=（t﹣2）2+16，
∴当t=2时，S有最小值是16；
（3）①假设∠FBD为直角，则点F在直线BC上∵PF=OP＜AB，
∴点F不可能在BC上，即∠FBD不可能为直角；
②假设∠FDB为直角，则点F在EF上，∵点D在矩形的对角线PE上，
∴点D不可能在EF上，即∠FDB不可能为直角；
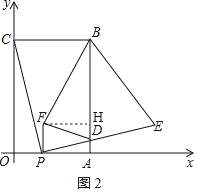
③假设∠BFD为直角且FB=FD，则∠FBD=∠FDB=45°如图2，作FH⊥BD于点H，
则FH=PA，即4﹣t=6﹣t，方程无解，
∴假设不成立，即△BDF不可能是等腰直角三角形．
