题目内容
【题目】如图，在五边形
中，
，
，
，
在
，
上分别找一点
，
，使得
的周长最小时，则
的度数为（ ）.
A. 
B. 
C. 
D. 
【答案】A
【解析】
取点A关于BC的对称点P，关于DE的对称点Q，连接PQ与BC交于点M，与DE交于点N，根据轴对称的性质可得AM=PM，AN=QN，然后求出
的周长=PQ，根据轴对称确定最短路线问题，PQ的长度即为的周长最小值，根据三角形内角和求出
，再根据三角形的外角定理求出
，
，即可求出答案.
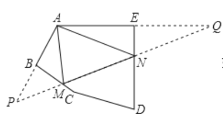
如图，取点A关于BC的对称点P，关于DE的对称点Q，连接PQ与BC交于点M，与DE交于点N
则AM=PM，AN=QN
∴
∴的周长=AM+MN+AN=PM+MN+QN=PQ
由轴对称确定最短路线，PQ的长度即为的周长最小值，
∵
∴
∵
∴
故选A.
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
相关题目
【题目】某出租车司机从公司出发，在东西方向的人民路上连续接送
批客人，行驶路程记录如下(规定向东为正，向西为负，单位:
):
第 | 第 | 第 | 第 | 第 |
|
|
|
|
|
（1）接送完第批客人后，该驾驶员在公司什么方向，距离公司多少千米?
（2）若该出租车每千米耗油
升，那么在这过程中共耗油多少升?
（3）若该出租车的计价标准为：行驶路程不超过
收费
元，超过的部分按每千米
元收费，在这过程中该驾驶员共收到车费多少元?
