题目内容
【题目】定义:若点P为四边形ABCD内一点,且满足∠APB+∠CPD=180°, 则称点P为四边形ABCD的一个“互补点”.
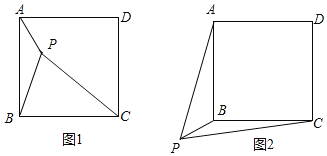
(1)如图1,点P为四边形ABCD的一个“互补点”,∠APD=63°,求∠BPC的度数.

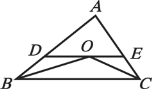
(2)如图2,点P是菱形ABCD对角线上的任意一点.求证:点P为菱形ABCD的一个“互补点”.

【答案】(1)117°;(2)证明见解析.
【解析】(1)根据点P为四边形ABCD的一个“互补点”的定义,可得出∠APD+∠BPC=180°,从而可求出结果;
(2)根据菱形的性质可证得AB=BC,∠ABP=∠CBP,再证明△ABP≌△CBP,可证得∠1=∠3,同理得出∠2=∠4,然后证明∠1+∠2=180°,即可求证.
(1)∵点P为四边形ABCD的一个“互补点”,∠APD=63°
∴∠APD+∠BPC=180°
∴∠BPC=180°-63°=117°
(2)证明:如图,连接AP、PC
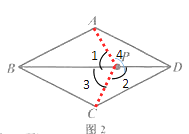
∵菱形ABCD
∴AB=BC,∠ABP=∠CBP
∵BP=BP
∴△ABP≌△CBP(SAS)
∴∠1=∠3
同理∠2=∠4
∵∠1+∠3+∠2+∠4=360°
∴2∠1+2∠2=360°
∴∠1+∠2=180°
∴点P为菱形ABCD的一个“互补点” .

练习册系列答案
相关题目