题目内容
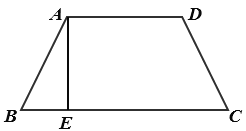
【题目】如图,已知在梯形 ABCD 中,AD//BC,AB=AD=CD=13,AE⊥BC,垂足为 E,AE=12,求边 BC 的长
【答案】23
【解析】
如图所示,作出辅助线,先证明AD=EF,再证明Rt△ABE≌Rt△DCF,得出BE=CF,
再由勾股定理求出即可.
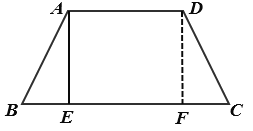
解:如图所示,过点D作DF⊥BC于点F,
∵AE⊥BC,
∴∠AEB=∠DFC=90°,
∴AE∥DF
又∵AD∥BC,
∴四边形ADFE是平行四边形,
∴AE=DF,EF=AD=13
在Rt△ABE与Rt△DCF中,
![]() ,
,
∴Rt△ABE≌Rt△DCF(HL)
∴BE=CF,
又∵AE=12,AB=13,
∴由勾股定理得:BE=![]() ,
,
∴BE=CF=5
∴BC=EF+BE+CF=13+5+5=23.

练习册系列答案
相关题目