题目内容
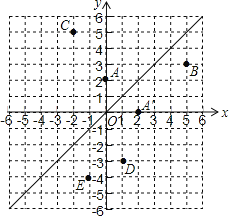
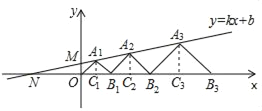
【题目】如图,在平面直角坐标系xOy中,点A1,A2,A3,…和B1,B2,B3,…分别在直线y=![]() x+
x+![]() 和x轴上,△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果A1(1,1),A2(
和x轴上,△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果A1(1,1),A2(![]() ,
,![]() ),那么点A3的纵坐标是( )
),那么点A3的纵坐标是( )
A. ![]() B. 2cm C.
B. 2cm C. ![]() D.
D. ![]()
【答案】D
【解析】
由直线y=![]() x+
x+![]() 求出直线与x轴、y轴的交点坐标,求出直线与x轴的夹角的正切值,分别过等腰直角三角形的直角顶点向x轴作垂线,然后根据等腰直角三角形斜边上的高线与中线重合并且等于斜边的一半,利用正切值列式依次求出三角形的斜边上的高线,即可得到A3的坐标.
求出直线与x轴、y轴的交点坐标,求出直线与x轴的夹角的正切值,分别过等腰直角三角形的直角顶点向x轴作垂线,然后根据等腰直角三角形斜边上的高线与中线重合并且等于斜边的一半,利用正切值列式依次求出三角形的斜边上的高线,即可得到A3的坐标.
∵直线 y=![]() x+
x+![]() 当x=0时,y=
当x=0时,y=![]() ,
,
当y=0时,![]() x+
x+![]() =0,解得x=-4,
=0,解得x=-4,
∴点M、N的坐标分别为M(0,![]() ),N(-4,0),
),N(-4,0),
∴tan∠MNO=![]() =
=![]() =
=![]() ,
,
∵A1(1,1),A2(![]() ,
,![]() ),
),
∴OB2=OB1+B1B2=2×1+2×![]() =2+3=5,
=2+3=5,
tan∠MNO=![]() ,
,
∵△B2A3B3是等腰直角三角形,
∴A3C3=B2C3,
∴A3C3=![]() ,
,
∴点A3的纵坐标是![]() ,
,
故选:D.

练习册系列答案
相关题目