题目内容
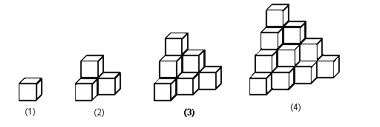
【题目】如图是由边长为1 的正方体搭成的立体图形，第（1）个图形由1个正方体搭成，第（2）个图形由4个正方体搭成，第（3）个图形由10个正方体搭成，以此类推，搭成第（6）个图形所需要的正方体个数是（ ）
A.84个B.56个C.37个D.36个
【答案】B
【解析】
根据图形的变换规律，可知第n个图形中的正方体的个数为1+3+6+…+
，据此可得第（6）个图形中正方体的个数．
由图可得：
第（1）个图形中正方体的个数为1；
第（2）个图形中正方体的个数为4=1+3；
第（3）个图形中正方体的个数为10=1+3+6；
第（4）个图形中正方体的个数为20=1+3+6+10；
故第n个图形中的正方体的个数为1+3+6+…+，
∴第（5）个图形中正方体的个数为1+3+6+10+15=35；
第（6）个图形中正方体的个数为1+3+6+10+15+21=56；
故选：B．
练习册系列答案
相关题目
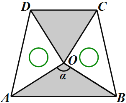
【题目】如图1，将边长为1的正方形ABCD压扁为边长为1的菱形ABCD．在菱形ABCD中，∠A的大小为α，面积记为S．
（1）请补全下表：
30° | 45° | 60° | 90° | 120° | 135° | 150° | |
S |
| 1 |
|
（2）填空：
由（1）可以发现正方形在压扁的过程中，菱形的面积随着∠A大小的变化而变化，不妨把菱形的面积S记为S(α)．例如：当α＝30°时，
；当α＝135°时，
．由上表可以得到
( ______°)；
( ______°)，…，由此可以归纳出
．
（3） 两块相同的等腰直角三角板按如图的方式放置，AD＝
，∠AOB＝α，试探究图中两个带阴影的三角形面积是否相等，并说明理由（注：可以利用（2）中的结论）．
