题目内容
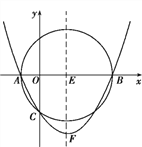
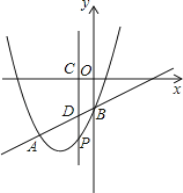
【题目】如图,抛物线y=x2+bx+c与直线y=x﹣1交于A、B两点.点A的横坐标为﹣3,点B在y轴上,点P是y轴左侧抛物线上的一动点,横坐标为m,过点P作PC⊥x轴于C,交直线AB于D.
(1)求抛物线的解析式;
(2)当m为何值时,S四边形OBDC=2S△BPD;
(3)是否存在点P,使△PAD是直角三角形?若存在,求出点P的坐标;若不存在,说明理由.

【答案】(1)y=x2+4x﹣1;(2)m=﹣![]() ,﹣2或
,﹣2或![]() 时S四边形OBDC=2S△BPD;
时S四边形OBDC=2S△BPD;
(3)P(﹣2,﹣5).
【解析】分析:(1)将x=0代入y=x-1求出B的坐标,将x=-3代入y=x-1求出A的坐标,由待定系数法就可以求出抛物线的解析式;
(2)由P点的横坐标为m可以表示出P、D的坐标,由此表示出S四边形OBDC和2S△BPD建立方程求出其解即可.
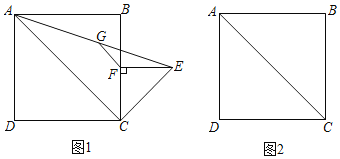
(3)如图2,当∠APD=90°时,设出P点的坐标,就可以表示出D的坐标,由△APD∽△FCD列出比例式求解即可;如图3,当∠PAD=90°时,作AE⊥x轴于E,根据比例式表示出AD,再由△PAD∽△FEA列出比例式求解.
详解:(1)∵y=x﹣1,
∴当x=0时,y=﹣1,
∴B(0,﹣1).
当x=﹣3时,y=﹣4,
∴A(﹣3,﹣4).
∵y=x2+bx+c与直线y=x﹣1交于A、B两点,
∴![]() ,
,
∴![]() ,
,
∴抛物线的解析式为:y=x2+4x﹣1;
(2)∵P点横坐标是m(m<0),
∴P(m,m2+4m﹣1),D(m,m﹣1)
如图1①,作BE⊥PC于E,

∴BE=﹣m.
CD=1﹣m,OB=1,OC=﹣m,CP=1﹣4m﹣m2,
∴PD=1﹣4m﹣m2﹣1+m=﹣3m﹣m2,
∴![]() ,
,
解得:m1=0(舍去),m2=﹣2,m3=﹣![]() ;
;
如图1②,作BE⊥PC于E,

∴BE=﹣m.
PD= m2+4m- 1-m+1= m2+3m,
∴![]() ,
,
解得:m=0(舍去)或m=![]() (正值舍去),
(正值舍去),
∴m=﹣![]() ,﹣2或
,﹣2或![]() 时S四边形OBDC=2S△BPD;
时S四边形OBDC=2S△BPD;
(3))如图2,

当∠APD=90°时,设P(m,m2+4m﹣1),则D(m,m﹣1),
∴AP=m+4,CD=1﹣m,OC=﹣m,CP=1﹣4m﹣m2,
∴DP=1﹣4m﹣m2﹣1+m=﹣3m﹣m2.
在y=x﹣1中,当y=0时,x=1,
∴(1,0),
∴OF=1,
∴CF=1﹣m.AF=4![]() .
.
∵PC⊥x轴,
∴∠PCF=90°,
∴∠PCF=∠APD,
∴CF∥AP,
∴△APD∽△FCD,![]() ,
,
∴![]() ,
,
解得:m=1(舍去)或m=﹣2,
∴P(﹣2,﹣5)
如图3,当∠PAD=90°时,作AE⊥x轴于E,
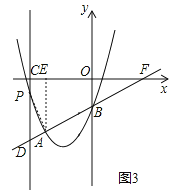
∴∠AEF=90°.CE=﹣3﹣m,EF=4,AF=4![]() ,PD=1﹣m﹣(1﹣4m﹣m2)=3m+m2.
,PD=1﹣m﹣(1﹣4m﹣m2)=3m+m2.
∵PC⊥x轴,
∴∠DCF=90°,
∴∠DCF=∠AEF,
∴AE∥CD.
∴![]() ,
,
∴AD=![]() (﹣3﹣m).
(﹣3﹣m).
∵△PAD∽△FEA,
∴![]() ,
,
∴![]() ,
,
∴m=﹣2或m=﹣3
∴P(﹣2,﹣5)或(﹣3,﹣4)与点A重合,舍去,
∴P(﹣2,﹣5).

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案