题目内容
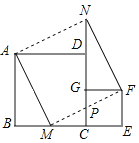
【题目】如图放置的两个正方形，大正方形ABCD边长为a，小正方形CEFG边长为b(a＞b),M在边BC上，且BM=b，连AM，MF，MF交CG于点P，将△ABM绕点A旋转至△ADN，将△MEF绕点F旋转至△NGF。给出以下五种结论：∠MAD=∠AND；CP= 
；ΔABM≌ΔNGF；④S四边形AMFN=a2+b2；⑤A，M，P，D四点共线
其中正确的个数是（ ）
A. 2 B. 3 C. 4 D. 5
【答案】D
【解析】试题解析：①∵四边形ABCD是正方形，∴∠BAD=∠ADC=∠B=90°，∴∠BAM+∠DAM=90°，∵将△ABM绕点A旋转至△ADN，∴∠NAD=∠BAM，∠AND=∠AMB，∴∠DAM+∠NAD=∠NAD+∠AND=∠AND+∠NAD=90°，∴∠DAM=∠AND，故①正确；
②∵四边形CEFG是正方形，∴PC∥EF，∴△MPC∽△EMF，∴
，∵大正方形ABCD边长为a，小正方形CEFG边长为b（a＞b），BM=b，∴EF=b，CM=a﹣b，ME=（a﹣b）+b=a，∴
，∴CP= 
；故②正确；
③∵将△MEF绕点F旋转至△NGF，∴GN=ME，∵AB=a，ME=a，∴AB=ME=NG，在△ABM与△NGF中，∵AB=NG=a，∠B=∠NGF=90°，GF=BM=b，∴△ABM≌△NGF；故③正确；
④∵将△ABM绕点A旋转至△ADN，∴AM=AN，∵将△MEF绕点F旋转至△NGF，∴NF=MF，∵△ABM≌△NGF，∴AM=NF，∴四边形AMFN是矩形，∵∠BAM=∠NAD，∴∠BAM+DAM=∠NAD+∠DAN=90°，∴∠NAM=90°，∴四边形AMFN是正方形，∵在Rt△ABM中，a2+b2=AM2，∴S四边形AMFN=AM2=a2+b2；故④正确；
⑤∵四边形AMFN是正方形，∴∠AMP=90°，∵∠ADP=90°，∴∠ABP+∠ADP=180°，∴A，M，P，D四点共圆，故⑤正确．
故选D．
