题目内容
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别角与A、B两点,P、Q分别是线段OB、AB上的两个动点,点P从O出发一每秒2个单位长度的速度向终点B运动,同时Q从B出发,以每秒5个单位的速度向终点A运动,当其中一点到达终点时整个运动结束,设运动时间为t秒。
轴分别角与A、B两点,P、Q分别是线段OB、AB上的两个动点,点P从O出发一每秒2个单位长度的速度向终点B运动,同时Q从B出发,以每秒5个单位的速度向终点A运动,当其中一点到达终点时整个运动结束,设运动时间为t秒。
(1)求出点Q的坐标(用t的代数式表示)
(2)若C为OA的中点,连接PQ、CQ,以PQ、CQ为邻边作![]() PQCD.
PQCD.
①是否存在时间t,使得坐标轴切好将![]() PQCD的面积分为1:5的两个部分,若存在,求出t的值;若不存在,请说明理由.
PQCD的面积分为1:5的两个部分,若存在,求出t的值;若不存在,请说明理由.
②直接写出整个运动过程中![]() PQCD对角线DQ的取值范围.
PQCD对角线DQ的取值范围.
【答案】(1)![]() ;(2)①t=1或1.5;②4
;(2)①t=1或1.5;②4![]() ≤DQ≤4
≤DQ≤4![]()
【解析】
(1)先利用勾股定理求出AB,再判断出△BEQ∽△BOA,得出比例式,代值求解即可得出结论;
(2)①分两种情况,利用同高的两三角形的面积的比等于底的比,求解得出结论;
②利用两点间距离公式,得出DQ2,再用函数的性质即可得出结论.
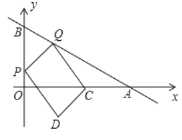
解:(1)如图1,
针对于直线y=![]() ,
,
令x=0,则y=6,
∴B(0,6),
∴OB=6,
令y=0,则![]() =0,
=0,
∴x=8,
∴A(8,0),
∴OA=8,
根据勾股定理得,AB=![]() =10,
=10,
由运动知,BQ=5t,
过点Q作QE⊥y轴于E,
∴QE∥AO,
∴△BEQ∽△BOA,
∴![]() ,
,
∴![]() ,
,
∴BQ=3t,EQ=4t,
∴OE=OB﹣BE=6﹣3t,
∴Q(4t,6﹣3t);
(2)连接DQ,CP,由运动知,OP=2t,
∴P(0,2t),
∵点C是OA的中点,
∴C(4,0),
∵四边形CQPD是平行四边形,
∴DQ与CP互相平分,
设D(m,n),
由(1)知,Q(4t,6﹣3t);
∴4t+m=4,6﹣3t+n=2t,
∴m=4﹣4t,n=5t﹣6,
∴D(4﹣4t,5t﹣6),
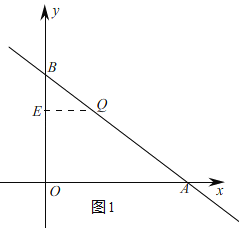
①Ⅰ、当x轴将将PQCD的面积分为1:5的两个部分时,如图2,
∵PC是平行四边形PQCD的对角线,
∴S△PCQ=S△PCD,
∵S△CDF:S四边形CFPQ=1:5,
∴S△CDF:S△CPF=1:2,
∴DF:PF=1:2,
∴PF:DF=2:1,
过点D作DG⊥y轴于G,
∴OG=6﹣5t,
∴DG∥FO,
∴![]() ,
,
∴![]() ,
,
∴t=1,【注:点D本身在y轴上,为了解决问题,没将点D放在y轴上】
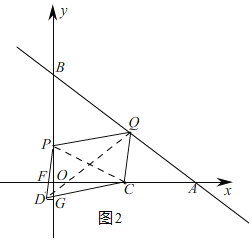
Ⅱ、当x轴将将PQCD的面积分为1:5的两个部分时,如图3,
过点D作DN⊥x轴于N,
同Ⅰ的方法得,t=1.5,
即:坐标轴刚好将PQCD的面积分为1:5的两个部分时,t=1秒或1.5秒;
②由(1)知,Q(4t,6﹣3t),
∵D(4﹣4t,5t﹣6),
∴DQ2=(4﹣4t﹣4t)2+(6﹣3t﹣5t+6)2=128(t﹣1)2+32,
由运动知,0≤t≤2,
∴当t=1时,DQ2最小=32,
∴DQ最小=4![]() ,
,
当t=0或2时,DQ2最大=160,
∴DQ最大=4![]() ,
,
∴4![]() ≤DQ≤4
≤DQ≤4![]() .
.

 阅读快车系列答案
阅读快车系列答案