Question

【题目】如图，△ABC中，AB=，AC=5，tanA=2，D是BC中点，点P是AC上一个动点，将△BPD沿PD折叠，折叠后的三角形与△PBC的重合部分面积恰好等于△BPD面积的一半，则AP的长为______．

Answer 1

【答案】2或5﹣

【解析】分两种情况：

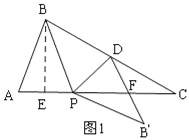
①当点B′在AC的下方时，如图1，

∵D是BC中点，∴S△BPD=S△PDC，

∵S△PDF=S△BPD，∴S△PDF=S△PDC，∴F是PC的中点，∴DF是△BPC的中位线，∴DF∥BP，

∴∠BPD=∠PDF，

由折叠得：∠BPD=∠B′PD，∴∠B′PD=∠PDF，∴PB′=B′D，即PB=BD，

过B作BE⊥AC于E，Rt△ABE中，tan∠A==2，

∵AB=，∴AE=1，BE=2，∴EC=5﹣1=4，

由勾股定理得：BC===2，

∵D为BC的中点，∴BD=，∴PB=BD=，

在Rt△BPE中，PE=1，∴AP=AE+PE=1=1=2；

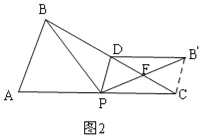
②当点B'在AC的上方时，如图2，连接B′C，

同理得：F是DC的中点，F是PB′的中点，∴DF=FC，PF=FB′，

∴四边形DPCB′是平行四边形，∴PC=B′D=BD=，∴AP=5﹣，

综上所述，AP的长为2或5﹣；

故答案为：2或5﹣．