题目内容
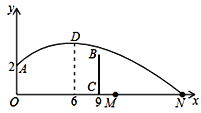
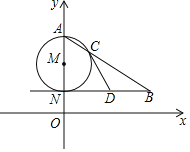
【题目】如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,经过A,D两点的圆的圆心F恰好在y轴上,⊙F与边BC相切于点E,与x轴交于点M,与y轴相交于另一点G,连接AE.
(1)求证:AE平分∠BAC;
(2)若点A,D的坐标分别为(0,﹣1),(2,0),求⊙F的半径;
(3)求经过三点M,F,D的抛物线的解析式.
【答案】(1)详见解析;(2)⊙F的半径为![]() ;(3)y=﹣
;(3)y=﹣![]() x2+
x2+![]() .
.
【解析】
(1)连接FE,先根据切线的性质知∠FEC=90°,结合∠C=90°证FE∥AC得∠EAC=∠FEA,根据FA=FE知∠FAE=∠FEA,从而得∠FAE=∠CAE,即可得证;
(2)连接FD,设⊙F的半径为r,根据FD2=(AF﹣AO)2+OD2知r2=(r﹣1)2+22,解之可得;
(3)根据圆的对称性得出点M的坐标,设抛物线的交点式,将点F坐标代入计算可得.
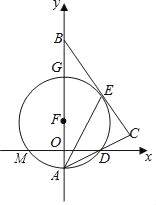
(1)连接FE,
∵⊙F与边BC相切于点E,
∴∠FEC=90°,
∵∠ACB=90°,
∴∠FEC+∠ACB=180°,
∴FE∥AC,
∴∠EAC=∠FEA,
∵FA=FE,
∴∠FAE=∠FEA,
∴∠FAE=∠CAE,
∴AE平分∠BAC;
(2)连接FD,
设⊙F的半径为r,
∵A(0,﹣1),D(2,0),
∴OA=1,OD=2,
在Rt△FOD中,FD2=(AF﹣AO)2+OD2,
∴r2=(r﹣1)2+22,
解得:r=![]() ,
,
∴⊙F的半径为![]() ;
;
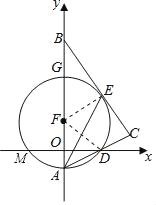
(3)∵FA=r=![]() ,OA=1,FO=
,OA=1,FO=![]() ,
,
∴F(0,![]() ),
),
∵直径AG垂直平分弦MD,点M和点D(2,0)关于y轴对称轴,
∴M(﹣2,0),
设抛物线解析式为y=a(x+2)(x﹣2),
将点F(0,![]() )代入,得:﹣4a=
)代入,得:﹣4a=![]() ,
,
解得:a=﹣![]() ,
,
则抛物线解析式为y=﹣![]() (x+2)(x﹣2)=﹣
(x+2)(x﹣2)=﹣![]() x2+
x2+![]() .
.

练习册系列答案
相关题目