题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以点
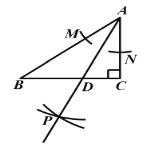
,以点![]() 为圆心,以任意长为半径作弧,分别交
为圆心,以任意长为半径作弧,分别交![]() 于点M,N,再分别以M,N为圆心,以大于
于点M,N,再分别以M,N为圆心,以大于![]() 的长为半径作弧,两弧交于点
的长为半径作弧,两弧交于点![]() ,作射线
,作射线![]() 交
交![]() 于点
于点![]() ,则
,则![]() 的长是__________.
的长是__________.
【答案】1.5
【解析】
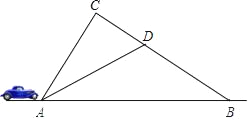
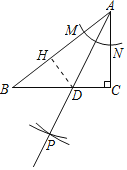
如图,作DH⊥AB于H.由△ADH≌△ADC(AAS),推出DH=DC,AC=AH=3,在Rt△ABC中,易知BC=![]() =4,设DC=DH=m,在Rt△BHD中,根据BD2=BH2+DH2,构建方程求出m即可.
=4,设DC=DH=m,在Rt△BHD中,根据BD2=BH2+DH2,构建方程求出m即可.
如图,作DH⊥AB于H.
∵DA平分∠BAC,
∴∠DAH=∠DAC,
∵∠AHD=∠C=90°,AD=AD,
∴△ADH≌△ADC(AAS),
∴DH=DC,AC=AH=3,
在Rt△ABC中,∵AB=5,AC=3,
∴BC=![]() =4,设DC=DH=m,
=4,设DC=DH=m,
在Rt△BHD中,∵BD2=BH2+DH2,
∴(4-m)2=m2+22,
∴m=![]() ,
,
∴CD=![]() ,
,
故答案为![]() .
.

【题目】某村在推进美丽乡村活动中,决定建设幸福广场,计划铺设相同大小规格的红色和蓝色地砖.经过调査.获取信息如下:
购买数量低于5000块 | 购买数量不低于5000块 | |
红色地砖 | 原价销售 | 以八折销售 |
蓝色地砖 | 原价销售 | 以九折销售 |
如果购买红色地砖4000块,蓝色地砖6000块,需付款86000元;如果购买红色地砖10000块,蓝色地砖3500块,需付款99000元.
(1)红色地砖与蓝色地砖的单价各多少元?
(2)经过测算,需要购置地砖12000块,其中蓝色地砖的数量不少于红色地砖的一半,并且不超过6000块,如何购买付款最少?请说明理由.
【题目】从甲、乙两位运动员中选出一名参加在规定时间内的投篮比赛.预先对这两名运动员进行了6次测试,成绩如下(单位:个):
甲:6,12,8,12,10,12;
乙:9,10,11,10,12,8;
(1)填表:
平均数 | 众数 | 方差 | |
甲 | 10 |
|
|
乙 |
| 10 |
|
(2)根据测试成绩,请你运用所学的统计知识作出分析,派哪一位运动员参赛更好?为什么?