题目内容
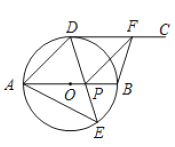
【题目】如图,在⊙O中,半径OC⊥弦AB于点D,点E为优弧AB上一点,连接AE、BE、AC,过点C的直线与EA延长线交于点F,且∠ACF=![]() ∠AEB.
∠AEB.
(1)求证:CF与⊙O相切;
(2)若∠AEB=60°,AB=4![]() ,求⊙O的半径;
,求⊙O的半径;
(3)在(2)的条件下,若AE=4![]() ,求EC的长.
,求EC的长.
【答案】(1)证明见解析;(2)4;(3)2![]() +2
+2![]() .
.
【解析】
(1)根据垂径定理得到弧AC=弧BC,求得∠FEC=∠BEC=![]() ∠AEB,等量代换得到∠ACF=∠BEC,推出AB∥CF,于是得到结论;
∠AEB,等量代换得到∠ACF=∠BEC,推出AB∥CF,于是得到结论;
(2)连接OA,根据圆周角定理得到∠AEC=30°,求得∠AOD=2∠AEC=60°,解直角三角形的即可得到结论;
(3)连接OE,过A作AH⊥CE于H,根据勾股定理的逆定理得到∠AOE=90°,根据圆周角定理得到∠ACE=![]() ∠AOE=45°,解直角三角形即可得到结论.
∠AOE=45°,解直角三角形即可得到结论.
(1)证明:∵半径OC⊥弦AB于点D,
∴弧AC=弧BC,
∴∠FEC=∠BEC=![]() ∠AEB,
∠AEB,
∵∠ACF=![]() ∠AEB,
∠AEB,
∴∠ACF=∠BEC,
∵∠BAC=∠BEC,
∴∠ACF=∠CAB,
∴AB∥CF,
∵OC⊥AB,
∴OC⊥CF,
∴CF与⊙O相切;
(2)解:连接OA,
∵∠AEB=60°,
∴∠AEC=30°,
∴∠AOD=2∠AEC=60°,
∴在Rt△AOD中,AD=![]() AB=2
AB=2![]() ,∠AOD=60°,
,∠AOD=60°,
∴OA=![]() =4,
=4,
∴⊙O的半径为4;
(3)解:连接OE,过A作AH⊥CE于H,
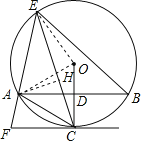
∵OE2+OA2=42+42=32=(4![]() )2=AE2,
)2=AE2,
∴∠AOE=90°,
∴∠ACE=![]() ∠AOE=45°,
∠AOE=45°,
在Rt△AEH中,∵∠AEH=30°,AE=4![]() ,
,
∴AH=2![]() ,EH=2
,EH=2![]() ,
,
在Rt△AHC中,∵∠ACH=45°,
∴CH=AH=2![]() ,
,
∴CE=CH+EH=2![]() +2
+2![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某村在推进美丽乡村活动中,决定建设幸福广场,计划铺设相同大小规格的红色和蓝色地砖.经过调査.获取信息如下:
购买数量低于5000块 | 购买数量不低于5000块 | |
红色地砖 | 原价销售 | 以八折销售 |
蓝色地砖 | 原价销售 | 以九折销售 |
如果购买红色地砖4000块,蓝色地砖6000块,需付款86000元;如果购买红色地砖10000块,蓝色地砖3500块,需付款99000元.
(1)红色地砖与蓝色地砖的单价各多少元?
(2)经过测算,需要购置地砖12000块,其中蓝色地砖的数量不少于红色地砖的一半,并且不超过6000块,如何购买付款最少?请说明理由.