题目内容
 等腰梯形ABCD中,AB∥CD,∠A=60°,AD=BC=CD=6cm.
等腰梯形ABCD中,AB∥CD,∠A=60°,AD=BC=CD=6cm.(1)请写∠BCD的度数(可直接写出).
(2)试求梯形ABCD的底边AB的长度.
(3)有一动点E以2cm/s的速度从C点出发,沿着DC的延长线向右运动,连接BE.当点E的运动时间t为多少秒时,△BEC恰好为直角三角形?
(4)有一动点E以2cm/s的速度从C点出发,沿着DC的延长线向右运动,同时有一动点N以1cm/s的速度从B点出发,沿着射线BC运动,连接EN.当运动过程中,△ECN的面积是否存在最大值,若存在,试求出时间t;若不存在,请说明理由.
分析:(1)根据等腰梯形同一底上的两个角相等可得∠ABC=60°,再根据两直线平行,同旁内角互补即可求解;
(2)过点D作DF∥BC,可以证明△ADF是等边三角形,四边形BCDF是平行四边形,根据等边三角形的三条边都相等以及平行四边形的对边相等即可得解;
(3)先求出∠BCE=60°,然后分①∠CEB=90°与②∠CBE=90°两种情况,根据30°角所对的直角边等于斜边的一半求出CE的长度,然后根据时间=路程÷速度进行计算;
(4)表示出CN的长度,过点N作NF⊥CE于点F,根据三角函数求出NF,然后利用三角形的面积列式表示出△ECN的面积,再根据二次函数的最值问题求解即可.
(2)过点D作DF∥BC,可以证明△ADF是等边三角形,四边形BCDF是平行四边形,根据等边三角形的三条边都相等以及平行四边形的对边相等即可得解;
(3)先求出∠BCE=60°,然后分①∠CEB=90°与②∠CBE=90°两种情况,根据30°角所对的直角边等于斜边的一半求出CE的长度,然后根据时间=路程÷速度进行计算;
(4)表示出CN的长度,过点N作NF⊥CE于点F,根据三角函数求出NF,然后利用三角形的面积列式表示出△ECN的面积,再根据二次函数的最值问题求解即可.
解答:解:(1)∵等腰梯形ABCD中,∠A=60°,
∴∠ABC=60°,
∵AB∥CD,
∴∠BCD=180°-∠ABC=180°-60°=120°;
(2)过点D作DF∥BC,
∵AB∥CD,
∴四边形BCDF是平行四边形,
∴BF=CD,DF=BC,
∵AD=BC,∠A=60°,
∴△ADF是等边三角形,
∴AF=AD,
∵AD=BC=CD=6cm,
∴AB=AF+CD=6+6=12cm;
(3)∵∠BCD=120°,
∴∠BCE=60°,
①∠CEB=90°时,∠CBE=90°-∠BCE=90°-60°=30°,
∴CE=
×BC,
即2t=
×6,
解得t=
秒,
②∠CBE=90°时,∠CEB=90°-∠BCE=90°-60°=30°,
∴CE=2BC,
即2t=2×6,
解得t=6秒;
综上所述,点E的运动时间t为
秒或6秒时,△BEC恰好为直角三角形;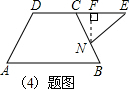
(4)∵点E的速度是2cm/s,点N的速度是1cm/s,
∴CE=2t,BN=t,
∴CN=BC-BN=6-t,
过点N作NF⊥CE于点F,则NF=CN•sin60°=
(6-t),
∴S△ECN=
×2t•
(6-t),
=
(-t2+6t),
=-
(t2-6t+9)+
,
=-
(t-3)2+
,
∴当t=3秒时,△ECN的面积最大,最大值是
.
∴∠ABC=60°,
∵AB∥CD,
∴∠BCD=180°-∠ABC=180°-60°=120°;
(2)过点D作DF∥BC,
∵AB∥CD,
∴四边形BCDF是平行四边形,

∴BF=CD,DF=BC,
∵AD=BC,∠A=60°,
∴△ADF是等边三角形,
∴AF=AD,
∵AD=BC=CD=6cm,
∴AB=AF+CD=6+6=12cm;
(3)∵∠BCD=120°,
∴∠BCE=60°,
①∠CEB=90°时,∠CBE=90°-∠BCE=90°-60°=30°,
∴CE=
| 1 |
| 2 |
即2t=
| 1 |
| 2 |
解得t=
| 3 |
| 2 |
②∠CBE=90°时,∠CEB=90°-∠BCE=90°-60°=30°,
∴CE=2BC,
即2t=2×6,
解得t=6秒;
综上所述,点E的运动时间t为
| 3 |
| 2 |

(4)∵点E的速度是2cm/s,点N的速度是1cm/s,
∴CE=2t,BN=t,
∴CN=BC-BN=6-t,
过点N作NF⊥CE于点F,则NF=CN•sin60°=
| ||
| 2 |
∴S△ECN=
| 1 |
| 2 |
| ||
| 2 |
=
| ||
| 2 |
=-
| ||
| 2 |
9
| ||
| 2 |
=-
| ||
| 2 |
9
| ||
| 2 |
∴当t=3秒时,△ECN的面积最大,最大值是
9
| ||
| 2 |
点评:本题考查了等腰梯形的性质,直角三角的性质,等边三角形的性质,二次函数的最值问题,等腰梯形的问题,准确作出辅助线往往是解题的关键.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
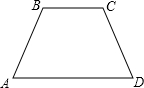
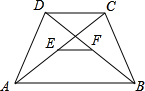 如图,在等腰梯形ABCD中,AB∥CD,∠ABC=60°,AC平分∠DAB,E、F分别为对角线AC、DB的中点,且EF=4.求这个梯形的面积.
如图,在等腰梯形ABCD中,AB∥CD,∠ABC=60°,AC平分∠DAB,E、F分别为对角线AC、DB的中点,且EF=4.求这个梯形的面积.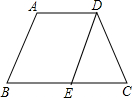 (1)如图,在等腰梯形ABCD中,AD∥BC,AB∥DE,BC=8,AD=5,求EC的长.
(1)如图,在等腰梯形ABCD中,AD∥BC,AB∥DE,BC=8,AD=5,求EC的长.
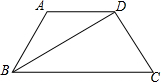 在等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠C=60°,
在等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠C=60°,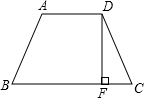 等腰梯形ABCD中,AD=2,BC=4,高DF=2,则腰CD长是
等腰梯形ABCD中,AD=2,BC=4,高DF=2,则腰CD长是