题目内容
 在等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠C=60°,
在等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠C=60°,(1)求AD:BC;
(2)若AD=2cm,求梯形ABCD的面积.
分析:(1根据平行线的性质推出∠ABD=∠DBC,得到∠ADB=∠ABD,求出AB=CD=AD,根据三角形的内角和定理求出∠BDC=90°,根据直角三角形性质求出即可;
(2)过D作DH⊥BC于H,过A作AE⊥BC于E,证平行四边形AEHD,推出AE=DH,证Rt△AEB≌Rt△DHC,推出BE=CH,求出DH,根据梯形的面积公式求出即可.
(2)过D作DH⊥BC于H,过A作AE⊥BC于E,证平行四边形AEHD,推出AE=DH,证Rt△AEB≌Rt△DHC,推出BE=CH,求出DH,根据梯形的面积公式求出即可.
解答:解:(1)∵AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ADB=∠ABD,
∴AD=AB=CD,
∵AD∥BC,AB=CD,
∴∠ABC=∠C=60°,
∴∠DBC=∠ABD=30°,
∴∠BDC=90°,
∴BC=2CD=2AD,
∴AD:BC=1:2,
答:AD:BC=1:2.
(2)过D作DH⊥BC于H,过A作AE⊥BC于E,
∵AD∥BC,DH⊥BC,AE⊥BC,
∴AE∥DH,
∴四边形AEHD是平行四边形,
∴AE=DH,
∵AB=CD,
∴Rt△AEB≌Rt△DHC,
∴BE=CH,
由勾股定理得:DH=
=
,
∴S梯形ABCD=
(AD+BC)×DH=
×(2+4)×
=3
(cm),
答:梯形ABCD的面积是3
cm.
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ADB=∠ABD,
∴AD=AB=CD,
∵AD∥BC,AB=CD,
∴∠ABC=∠C=60°,
∴∠DBC=∠ABD=30°,
∴∠BDC=90°,
∴BC=2CD=2AD,
∴AD:BC=1:2,
答:AD:BC=1:2.
(2)过D作DH⊥BC于H,过A作AE⊥BC于E,
∵AD∥BC,DH⊥BC,AE⊥BC,

∴AE∥DH,
∴四边形AEHD是平行四边形,
∴AE=DH,
∵AB=CD,
∴Rt△AEB≌Rt△DHC,
∴BE=CH,
由勾股定理得:DH=
| 22-12 |
| 3 |
∴S梯形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
答:梯形ABCD的面积是3
| 3 |
点评:本题主要考查对等腰梯形的性质,全等三角形的性质和判定,勾股定理,含30度角的直角三角形,平行线的性质,等腰三角形的判定等知识点的理解何志武,综合运用这些性质进行推理是解此题的关键.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且
25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且 24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.
24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.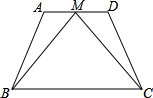 如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,MB=MC吗?为什么?
如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,MB=MC吗?为什么? 如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.
如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.