题目内容
 等腰梯形ABCD中,AD=2,BC=4,高DF=2,则腰CD长是
等腰梯形ABCD中,AD=2,BC=4,高DF=2,则腰CD长是| 5 |
| 5 |
分析:先过A作AE⊥BC于E,证平行四边形ADFE和△AEB≌△DFC,推出EF=AD,AE=DF,求出CF长,根据勾股定理即可求出CD的长.
解答: 解:过A作AE⊥BC于E,
解:过A作AE⊥BC于E,
∵DF⊥BC,
∴∠AEB=∠DFC=90°,DF∥AE,
∵AD∥BC,
∴四边形ADFE是平行四边形,
∴AD=EF=2,AE=DF,
∵AD∥BC,AB=CD,
∴∠B=∠C,
∵AE=DF,∠AEB=∠DFC,
∴△AEB≌△DFC,
∴BE=CF=
(BC-AD)=1,
在△DFC中,由勾股定理得:DC=
=
=
,
故答案为:
.
 解:过A作AE⊥BC于E,
解:过A作AE⊥BC于E,∵DF⊥BC,
∴∠AEB=∠DFC=90°,DF∥AE,
∵AD∥BC,
∴四边形ADFE是平行四边形,
∴AD=EF=2,AE=DF,
∵AD∥BC,AB=CD,
∴∠B=∠C,
∵AE=DF,∠AEB=∠DFC,
∴△AEB≌△DFC,
∴BE=CF=
| 1 |
| 2 |
在△DFC中,由勾股定理得:DC=
| DF2+CF2 |
| 22+12 |
| 5 |
故答案为:
| 5 |
点评:本题主要考查了等腰梯形的性质,用到的知识点是平行四边形的性质和判定,全等三角形的性质和判定,勾股定理,综合运用这些性质进行推理是解此题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目

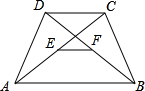 如图,在等腰梯形ABCD中,AB∥CD,∠ABC=60°,AC平分∠DAB,E、F分别为对角线AC、DB的中点,且EF=4.求这个梯形的面积.
如图,在等腰梯形ABCD中,AB∥CD,∠ABC=60°,AC平分∠DAB,E、F分别为对角线AC、DB的中点,且EF=4.求这个梯形的面积. (1)如图,在等腰梯形ABCD中,AD∥BC,AB∥DE,BC=8,AD=5,求EC的长.
(1)如图,在等腰梯形ABCD中,AD∥BC,AB∥DE,BC=8,AD=5,求EC的长.
 在等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠C=60°,
在等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠C=60°,