题目内容
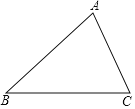
【题目】如图①,![]() 中,
中,![]() ,点
,点![]() 分别在边
分别在边![]() 上,
上,![]() 连接
连接![]() ,点
,点![]() 分别为
分别为![]() 的中点.
的中点.
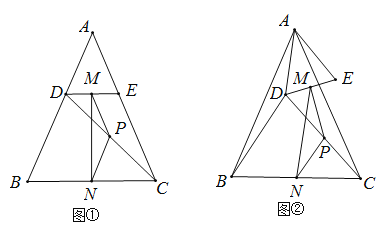
[观察猜想]图①,线段![]() 与
与![]() 的数量关系是 ,
的数量关系是 ,![]() _____
_____![]() ;
;
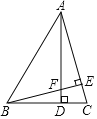
[探究证明]把![]() 绕点
绕点![]() 逆时针方向旋转到图②的位置,连结
逆时针方向旋转到图②的位置,连结![]() ,上述猜想的结论是否成立,请说明理由.
,上述猜想的结论是否成立,请说明理由.
【答案】[观察猜想]![]() ,
,![]() ;[探究证明]成立,理由见解析.
;[探究证明]成立,理由见解析.
【解析】
(1)根据中位线的性质得出MP=![]() CE,PN=
CE,PN=![]() BD,再根据AB=AC,且AD=AE,得出BD=CE,即可证明PN=PM;先求出∠B=∠ACB=
BD,再根据AB=AC,且AD=AE,得出BD=CE,即可证明PN=PM;先求出∠B=∠ACB=![]() =66°,∠B+∠BDC+∠DCB=180°,再根据MP∥CE,PN∥DB,得出∠DPN=180°-∠BDC,∠MPD=∠ECD,即可求出∠MPN;
=66°,∠B+∠BDC+∠DCB=180°,再根据MP∥CE,PN∥DB,得出∠DPN=180°-∠BDC,∠MPD=∠ECD,即可求出∠MPN;
(2)连接CE,先证明△BAD≌△CAE,然后根据中位线的性质得到MP=![]() CE=
CE=![]() BD,PN=
BD,PN=![]() BD,即可证明MP=PN;根据∠DBC+∠BCD+∠BDC=180°,且∠DBC=∠ABC-∠ABD=66°-∠ABD,∠BCD=∠ACB-∠ACD=66°-∠ACD,推出∠BDC=48°+∠DCE,再根据MP∥CE,PN∥DB,可得∠MPD=∠ECD,∠NPD=180°-∠PDB,即可求出∠MPN.
BD,即可证明MP=PN;根据∠DBC+∠BCD+∠BDC=180°,且∠DBC=∠ABC-∠ABD=66°-∠ABD,∠BCD=∠ACB-∠ACD=66°-∠ACD,推出∠BDC=48°+∠DCE,再根据MP∥CE,PN∥DB,可得∠MPD=∠ECD,∠NPD=180°-∠PDB,即可求出∠MPN.
解:(1)∵M,P分别为DE,CD中点,
∴MP∥CE且MP=![]() CE,
CE,
∵P,N分别为CD,BC中点,
∴PN∥BD且PN=![]() BD,
BD,
∵AB=AC,且AD=AE,
又∵BD=AB-AD,CE=AC-AE,
∴BD=CE,
∴PN=PM,
∵∠A=48°,且AB=AC,
∴∠B=∠ACB=![]() =66°,∠B+∠BDC+∠DCB=180°,
=66°,∠B+∠BDC+∠DCB=180°,
∴∠BDC-∠DCE=48°,
∵MP∥CE,PN∥DB,
∴∠DPN=180°-∠BDC,∠MPD=∠ECD,
∴∠MPN=∠MPD+∠DPN=180°-(∠BDC-∠ECD)=132°;
(2)成立,
如图,连接CE,
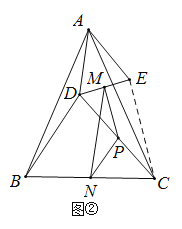
∵∠BAC=∠DAE=48°,且∠DAE=∠DAC+∠CAE,∠BAC=∠BAD+∠DAC,
∴∠BAD=∠CAE,
∵AD=AE,AB=AC,
∴△BAD≌△CAE(SAS),
∴CE=BD,∠ECA=∠ABD,
∵M,P,N分别为DE,DC,BC中点,
∴MP=![]() CE=
CE=![]() BD,PN=
BD,PN=![]() BD,
BD,
∴MP=PN,
∵∠DBC+∠BCD+∠BDC=180°,且∠DBC=∠ABC-∠ABD=66°-∠ABD,∠BCD=∠ACB-∠ACD=66°-∠ACD,
∴∠BDC=180°-66°-66°+∠ABD+∠ACD
=48°+∠ABD+∠ACD
=48°+∠ACE+∠ACD
∴∠BDC=48°+∠DCE,
∵MP∥CE,PN∥DB,
∴∠MPD=∠ECD,∠NPD=180°-∠PDB,
∴∠MPN=∠MPD+∠NPD=180°-∠PDB+∠ECD=180°-(48°+∠DCE)+∠ECD=180°-48°=132°,
∴猜想成立.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案【题目】某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作.已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果每千克的利润为3元,那么每天可售出250千克.
小红:如果以13元/千克的价格销售,那么每天可获取利润750元.
【利润=(销售价-进价)![]() 销售量】
销售量】
(1)请根据他们的对话填写下表:
销售单价x(元/kg) | 10 | 11 | 13 |
销售量y(kg) |
(2)请你根据表格中的信息判断每天的销售量y(千克)与销售单价x(元)之间存在怎样的函数关系.并求y(千克)与x(元)(x>0)的函数关系式;
(3)设该超市销售这种水果每天获取的利润为W元,求W与x的函数关系式.当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?
【题目】通过课本上对函数的学习,我们积累了一定的经验,下表是一个函数的自变量![]() 与函数值
与函数值![]() 的部分对应值,请你借鉴以往学习函数的经验,探究下列问题:
的部分对应值,请你借鉴以往学习函数的经验,探究下列问题:
| … | 0 | 1 | 2 | 3 | 4 | 5 | … |
| … | 6 | 3 | 2 | 1.5 | 1.2 | 1 | … |
(1)当![]() 时,
时,![]() ;
;
(2)根据表中数值描点![]() ,并画出函数图象;
,并画出函数图象;
(3)观察画出的图象,写出这个函数的一条性质: .