题目内容
【题目】已知，如图，在平面直角坐标系中，直线
与
轴交于点A，与
轴交于点B，抛物线
经过A、B两点，与轴的另一个交点为C．
（1）直接写出点A和点B的坐标；
（2）求抛物线的函数解析式；
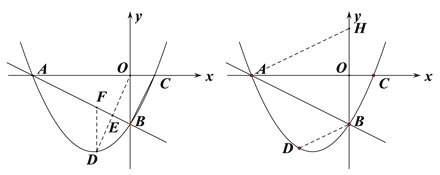
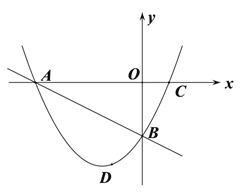
（3）D为直线AB下方抛物线上一动点；
①连接DO交AB于点E，若DE：OE=3：4，求点D的坐标；
②是否存在点D，使得∠DBA的度数恰好是∠BAC度数2倍，如果存在，求点D 的坐标，如果不存在，说明理由．
【答案】（1）A(-4，0)、B（0，-2）；（2）
；（3）①（-1，3）或（-3，-2）；②（-2，-3）．
【解析】
（1）在
中由
求出对应的x的值，由x=0求出对应的y的值即可求得点A、B的坐标；
（2）把（1）中所求点A、B的坐标代入
中列出方程组，解方程组即可求得b、c的值，从而可得二次函数的解析式；
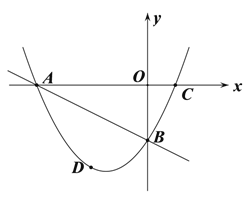
（3）①如图，过点D作x轴的垂线交AB于点F，连接OD交AB于点E，由此易得△DFE∽OBE，这样设点D的坐标为
，点F的坐标为
,结合相似三角形的性质和DE：OE=3:4，即可列出关于m的方程，解方程求得m的值即可得到点D的坐标；
②在y轴的正半轴上截取OH=OB，可得△ABH是等腰三角形，由此可得∠HAB=2∠BAC，若此时∠DAB =2∠BAC=∠HAB，则BD∥AH，再求出AH的解析式可得BD的解析式，由BD的解析式和抛物线的解析式联立构成方程组，解方程组即可求得点D的坐标．
解：（1）在中，由可得：
，解得：
；
由
可得：
，
∴点A的坐标为（-4，0），点B的坐标为（0，-2）；
（2）把点A的坐标为（-4，0），点B的坐标为（0，-2）代入得：
，解得：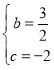
，
∴抛物线的解析式为：
；
（3）①过点D作x轴的垂线交AB于点F，
设点D，F,
连接DO交AB于点E，△DFE∽OBE，
因为DE：OE=3：4，
所以FD：BO=3：4，
即：FD=
BO=
,
所以
,
解之得： m1=-1，m2=-3 ，
∴D的坐标为（-1，3）或（-3，-2）；
②在y轴的正半轴上截取OH=OB，可得△ABH是等腰三角形，
∴∠BAH=2∠BAC，
若∠DBA=2∠BAC，则∠DBA=∠BAH，
∴AH//DB，
由点A的坐标（-4，0）和点H的坐标（0，2）求得直线AH的解析式为：
，
∴直线DB的解析式是：
,
将：
联立可得方程组：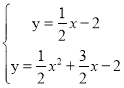
，
解得：
，
∴点D的坐标（-2，-3）．
