Question

【题目】如图，正方形ABCD中，AB=4，点E是边BC的中点，点G，H分别是边CD，AB上的动点，连接GH交AE于F，且使GH⊥AE，连接AG，EH，则EH+AG的最小值是（ ）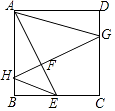

A.8
B.4
C.2
D.8

Answer 1

【答案】C
【解析】如图，由题意易证AE=GH=2 ，设FH=x，EF=y，则有HE+AG= + ，

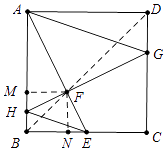
欲求HE+AG的最小值，相当于在平面直角坐标系内找一点（x，y），使得这个点到O（0，0），P（2 ，2 ）的距离和最小，显然这个点在线段OP上，满足x=y时，HE+AG的值最小，由此可知FH=EF时，HE+AG的值最小，如图连接BD交AE于F，作FM⊥AB于M，FN⊥BC于N，易证△FMH≌△FNE，

∴FH=EF，此时HE+AG的值最小，

易证四边形BNFM是正方形，设边长为a，则有 = ，

∴ = ，

∴a= ，

∴EF=FH= = ，

∴x=y= ，

∴HE+AG的最小值=2 ，

所以答案是：C．

解法二：作GK⊥AB于K，作EM∥AG，GM∥AE，则四边形AEGM是平行四边形．

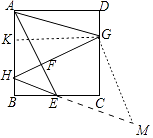
∵AE⊥HG，

∴∠B=∠GKH=∠AFH=90°，

∴∠BAE+∠AHF=90°，∠AHF+∠KGH=90°，

∴∠BAE=∠KGH，

∵KG=BC=AB，

∴△KGH≌△BAE，

∴GH=AG，

∴AE=GM=HG，AG=EM，

∴△GHM是等腰直角三角形，GH=GM=AE=2 ，

∵AG+HE=EM+EG，

∴当H、E、M共线时，AG+HE的值最小，最小值= HG=2 ．

所以答案是：C．

【考点精析】通过灵活运用正方形的性质和轴对称-最短路线问题，掌握正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形；已知起点结点，求最短路径；与确定起点相反，已知终点结点，求最短路径；已知起点和终点，求两结点之间的最短路径；求图中所有最短路径即可以解答此题．