题目内容
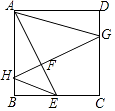
【题目】如图，梯形ABCD中，AD∥BC，∠C=90°，AB=AD=4，BC=6，以点A为圆心在梯形内画出一个最大的扇形，则阴影部分的面积为 ．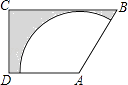 
【答案】10 
﹣4π
【解析】解：如图设扇形与BC相切于点E，连接AE，则AE⊥BC．
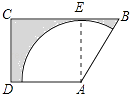
∵AD∥BC，∠C=90°，
∴∠D=∠C=∠AEC=90°，
∴四边形ADCE是矩形，
∴AD=CE=4，
∵BC=6，
∴BE=2，
在RT△AEB中，∵∠AEB=90°，AB=4，EB=2，
∴AE= 
=2 ，AB=2EB，
∴∠EAB=30°，
∵∠DAE=90°，
∴∠DAB=120°，
∴S阴=S梯形ABCD﹣ 
= 
（4+6） 
﹣ 
=10 ﹣4π．
所以答案是10 ﹣4π
【考点精析】根据题目的已知条件，利用扇形面积计算公式的相关知识可以得到问题的答案，需要掌握在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）．
练习册系列答案
相关题目
【题目】A，B，C三名大学生竞选系学生会主席，他们的笔试成绩和口试成绩（单位：分）分别用了两种方式进行了统计，如表和图一：
A | B | C | |
笔试 | 85 | 95 | 90 |
口试 | 80 | 85 |
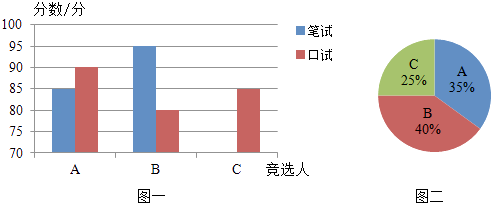
（1）请将表一和图一中的空缺部分补充完整．
（2）竞选的最后一个程序是由本系的300名学生进行投票，三位候选人的得票情况如图二（没有弃权票，每名学生只能推荐一个），请计算每人的得票数．
（3）若每票计1分，系里将笔试、口试、得票三项测试得分按4：3：3的比例确定个人成绩，请计算三位候选人的最后成绩，并根据成绩判断谁能当选．