题目内容
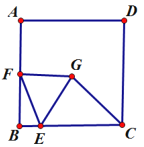
【题目】如图,点C为线段AB上一点,分别以AB、AC、CB为底作顶角为120°的等腰三角形,顶角顶点分别为D、E、F(点E、F在AB的同侧,点D在另一侧)
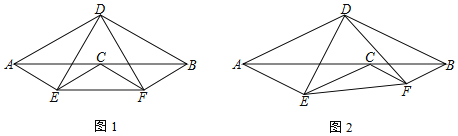
(1)如图1,若点C是AB的中点,则∠CED=______°;
(2)如图2.若点C不是AB的中点
①求证:△DEF为等边三角形;
②连接CD,若∠ADC=90°,AD=![]() ,请求出DE的长.
,请求出DE的长.
【答案】(1)30°;(2)①见解析;②![]()
【解析】
(1)如图1,作辅助线,构建高线,根据等腰三角形三线合一的性质得DC=AE=CE,证明∠HED=∠EDC=∠CED,由∠CEH=60°得∠DEC=30°;
(2)①作辅助线,构建等边三角形AEH,先证明四边形BDHF、四边形AECH是平行四边形,得对边相等,再证明△AEH是等边三角形,由SAS证明△DHE≌△FCE,可得DE=EF,∠DEH=∠FEC,所以△DEF是等边三角形;
②过E作EM⊥AB于M,由∠ADC=90°,∠DAC=30°,AD=![]() 得∠ACD=60°,CD=1,AC=2,再证CD=BC=1,证∠ECD=90°,由AE=CE得CM=
得∠ACD=60°,CD=1,AC=2,再证CD=BC=1,证∠ECD=90°,由AE=CE得CM=![]() AC=1,CE=
AC=1,CE=![]() ,利用勾股定理求出DE=
,利用勾股定理求出DE=![]()
![]()
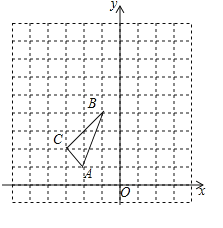
解:(1)如图1,过E作EH⊥AB于H,连接CD,
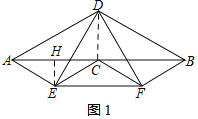
设EH=x,则AE=2x,AH=![]() x,
x,
∵AE=EC,
∴AC=2AH=2![]() x,
x,
∵C是AB的中点,AD=BD,
∴CD⊥AB,
∵∠ADB=120°,
∴∠DAC=30°,
∴DC=2x,
∴DC=CE=2x,
∵EH∥DC,
∴∠HED=∠EDC=∠CED,
∵∠CEH=60°,
∴∠DEC=30°,
故答案为:30°;
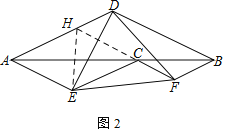
(2)①如图2,延长FC交AD于H,连接HE,
∵CF=FB,
∴∠FCB=∠FBC,
∵∠CFB=120°,
∴∠FCB=∠FBC=30°,
同理:∠DAB=∠DBA=30°,∠EAC=∠ECA=30°,
∴∠DAB=∠ECA=∠FBD,
∴AD∥EC∥BF,
同理AE∥CF∥BD,
∴四边形BDHE、四边形AECH是平行四边形,
∴EC=AH,BF=HD,
∵AE=EC,
∴AE=AH,
∵∠HAE=60°,
∴△AEH是等边三角形,
∴AE=AH=HE=CE,∠AHE=∠AEH=60°,
∴∠DHE=120°,
∴∠DHE=∠FCE.
∵DH=BF=FC,
∴△DHE≌△FCE(SAS),
∴DE=EF,∠DEH=∠FEC,
∴∠DEF=∠CEH=60°,
∴△DEF是等边三角形;
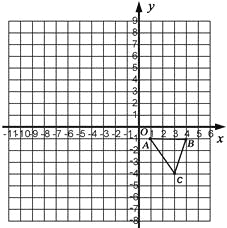
②如图3,过E作EM⊥AB于M,
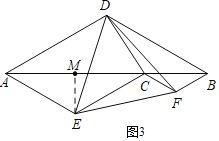
∵∠ADC=90°,∠DAC=30°,AD=![]() ,
,
∴∠ACD=60°,CD=1,AC=2,
∵∠DBA=30°,
∴∠CDB=∠DBC=30°,
∴CD=BC=1,
∵∠ACE=30°,∠ACD=60°,
∴∠ECD=30°+60°=90°,
∵AE=CE,
∴CM=![]() AC=1,
AC=1,
∵∠ACE=30°,
∴CE=![]() ,
,
Rt△DEC中,DE=![]() =
=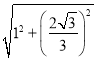 =
=![]() .
.

【题目】垫球是排球队常规训练的重要项目之一,也是我市初中体育学业水平考试的一个选考项目.下列图表中的数据是从九年级一班、二班各随机抽取五名学生垫球测试成绩:
测试学生序号 | ① | ② | ③ | ④ | ⑤ |
一班 | 7 | 8 | 6 | 7 | 7 |
二班 | 4 | 8 | 7 | 10 | 6 |
解答下列问题:
(1)一班五名学生的测试成绩的众数是 ,二班五名学生的测试成绩的中位数是 .
(2)请你在图中补全二班五名学生的垫球测试成绩的折线统计图.从题中的信息,估计 班的垫球成绩要稳定.
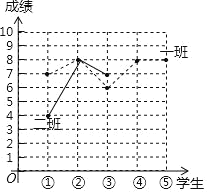
(3)把前三次对应序号下一班学生的垫球测试成绩减去二班学生垫球测试成绩,分别可得到数字3、0、﹣1,从这三个数中任意选取两个数组成有序数对(x,y),请用列表法或画树状图法列出可能出现的结果,并计算点(x,y)落在二次函数y=x2﹣1的图象上的概率.