题目内容
【题目】为迎接国庆节，某商店购进了一批成本为每件30元的纪念商品．经调查发现，该商品每天的销售量
（件
与销售单价
（元满足一次函数关系，其图象如图所示．
（1）求该商品每天的销售量与销售单价的函数关系式；
（2）若商店按不低于成本价，且不高于60元的单价销售，则销售单价定为多少，才能使销售该商品每天获得的利润
（元最大？最大利润是多少？
【答案】（1）
；（2）销售单价定为55元时，该商店每天获得的利润最大，最大利润是1250元.
【解析】
(1)将点(30，100)、(45,700)代入--次函数表达式,即可求解；
(2)由题意得
,即可求解.
（1）设销售量
与销售单价
之间的函数关系式为
，
将点
、
代入，得
.
解得
.
∴函数的关系式为：
（2）由题意得
，且30≤x≤60.
当
时，
取得最大值，此时
.
∴销售单价定为55元时，该商店每天获得的利润最大，最大利润是1250元.
期末集结号系列答案
【题目】某地质量监管部门对辖区内的甲、乙两家企业生产的某同类产品进行检查，分别随机抽取了50件产品并对某一项关键质量指标做检测，获得了它们的质量指标值s，并对样本数据（质量指标值s）进行了整理、描述和分析.下面给出了部分信息.
a.该质量指标值对应的产品等级如下：
质量指标值 |
|
|
|
|
|
等级 | 次品 | 二等品 | 一等品 | 二等品 | 次品 |
说明：等级是一等品，二等品为质量合格（其中等级是一等品为质量优秀）.
等级是次品为质量不合格.
b.甲企业样本数据的频数分布统计表如下（不完整）.
c.乙企业样本数据的频数分布直方图如下.
甲企业样本数据的频数分布表
分组 | 频数 | 频率 |
| 2 | 0.04 |
| m | |
| 32 | n |
| 0.12 | |
| 0 | 0.00 |
合计 | 50 | 1.00 |
乙企业样本数据的频数分布直方图
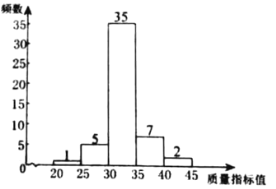
d.两企业样本数据的平均数、中位数、众数、极差、方差如下：
平均数 | 中位数 | 众数 | 极差 | 方差 | |
甲企业 | 31.92 | 32.5 | 34 | 15 | 11.87 |
乙企业 | 31.92 | 31.5 | 31 | 20 | 15.34 |
根据以上信息，回答下列问题：
（1）m的值为________，n的值为________.
（2）若从甲企业生产的产品中任取一件，估计该产品质量合格的概率为________；若乙企业生产的某批产品共5万件，估计质量优秀的有________万件；
（3）根据图表数据，你认为________企业生产的产品质量较好，理由为______________.（从某个角度说明推断的合理性）
