题目内容
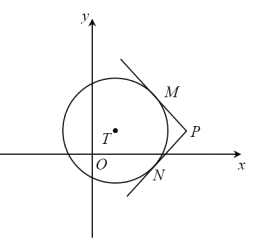
【题目】如图,在平面直角坐标系xOy中,过⊙T外一点P引它的两条切线,切点分别为M,N,若![]() ,则称P为⊙T的环绕点.
,则称P为⊙T的环绕点.
(1)当⊙O半径为1时,
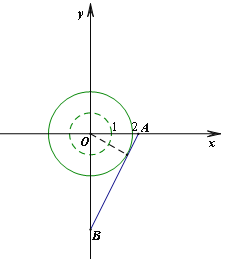
①在![]() 中,⊙O的环绕点是___________;
中,⊙O的环绕点是___________;
②直线y=2x+b与x轴交于点A,y轴交于点B,若线段AB上存在⊙O的环绕点,求b的取值范围;
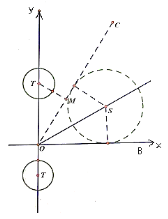
(2)⊙T的半径为1,圆心为(0,t),以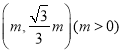 为圆心,
为圆心,![]() 为半径的所有圆构成图形H,若在图形H上存在⊙T的环绕点,直接写出t的取值范围.
为半径的所有圆构成图形H,若在图形H上存在⊙T的环绕点,直接写出t的取值范围.
【答案】(1)①![]() .②b的取值范围为
.②b的取值范围为![]() 或
或![]() .(2)
.(2)![]()
【解析】
(1)①根据环绕点的定义及作图找到![]() 即可判断;
即可判断;
②当点B在y轴正半轴上时,根据环绕点的定义考虑以下两种特殊情况:线段AB与半径为2的⊙O相切时,与当点B经过半径为1的⊙O时,分别求出此时的OB的长,即可得到可得b的取值范围,再由点B在y轴负半轴上时同理可得b的取值;
(3)根据题意作出图形,求出OS与x轴正半轴的夹角为30°,得∠BOC=60°,图形H为射线OB与射线OC围成的一个扇形区域(不包括点O,半径可无穷大),分当t≥0与t<0时,根据环绕点的定义进行求解.
(1)①如图,
∵P1在圆上,故不是环绕点,
P2引圆两条切线的夹角为90°,满足![]() ,故为⊙O的环绕点
,故为⊙O的环绕点
P3(0,2),∵P3O=2OM,∠P3MO=90°,∴∠MOP3=30°,
同理:∠NOP3=30°,∴![]() ,故为⊙O的环绕点
,故为⊙O的环绕点
故填:![]() ;
;
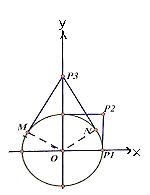
②半径为1的⊙O的所有环绕点在以O为圆心,半径分别为1和2的两个圆之间(如下图阴影部分所示,含大圆,不含小圆).
ⅰ)当点B在y轴正半轴上时,如图1,图2所示.
考虑以下两种特殊情况:线段AB与半径为2的⊙O相切时,![]() ;
;
当点B经过半径为1的⊙O时,OB=1.
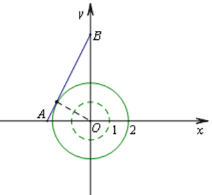
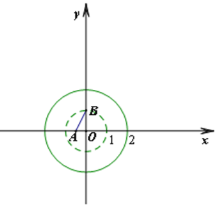
因为线段AB上存在⊙O的环绕点,所以可得b的取值范围为 ![]() ;
;
②当点B在y轴负半轴上时,如图3,图4所示.
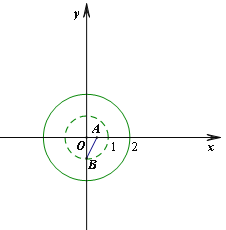
同理可得b的取值范围为 ![]() .
.
综上,b的取值范围为![]() 或
或![]() .
.
(3)点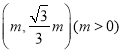 记为S,设OS与x轴正半轴的夹角为a
记为S,设OS与x轴正半轴的夹角为a
∵tana=![]()
∴a=30°,
如图,圆S与x轴相切,过O点作⊙S的切线OC,
∵OC、OB都是⊙S的切线
∴∠BOC=2∠SOB=60°,
当m取遍所有整数时 ,就形成图形H,
图形H为射线OB与射线OC围成的一个扇形区域(不包括点O,半径可无穷大)
当t≥0时,过T作OC的垂线,垂足为M,当TM>2时,图形H不存在环绕点,OT=2TM,故t≤4,
当t<0时,图形H上的点到T的距离都大于OT,当OT≥2时,图形H不存在⊙T环绕点,因此t>-2,
综上:![]() .
.

 考前必练系列答案
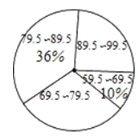
考前必练系列答案【题目】为了解学生的课外阅读情况,七(1)班针对“你最喜爱的课外阅读书目”进行调查(每名学生必须选一类且只能选一类阅读书目),并根据调查结果列出统计表,绘制成扇形统计图.
男、女生所选类别人数统计表
类别 | 男生(人) | 女生(人) |
文学类 | 12 | 8 |
史学类 |
| 5 |
科学类 | 6 | 5 |
哲学类 | 2 |
|

根据以上信息解决下列问题
(1)![]() ,
,![]() ;
;
(2)扇形统计图中“科学类”所对应扇形圆心角度数为 ![]() ;
;
(3)从选哲学类的学生中,随机选取两名学生参加学校团委组织的辩论赛,请用树状图或列表法求出所选取的两名学生都是男生的概率.
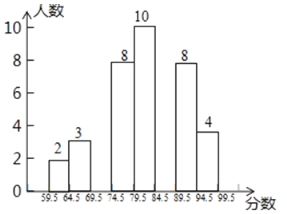
【题目】某同学所在年级的500名学生参加志愿者活动,现有以下5个志愿服务项目:A,纪念馆志讲解员.B.书香社区图书整理C.学编中国结及义卖.D,家风讲解员E.校内志愿服务,要求:每位学生都从中选择一个项目参加,为了了解同学们选择这个5个项目的情况,该同学随机对年级中的40名同学选择的志愿服务项目进行了调查,过程如下:
收集数据:设计调查问卷,收集到如下数据(志愿服务项目的编号,用字母代号表示)
B,E,B,A,E,C,C,C,B,B,
A,C,E,D,B,A,B,E,C,A,
D,D,B,B,C,C,A,E,B
C,B,D,C,A,C,C,A,C,E,
(1)整理、描述诗句:划记、整理、描述样本数据,绘制统计图如下,请补全统计表和统计图

选择各志愿服务项目的人数统计表
志愿服务项目 | 划记 | 人数 |
A.纪念馆志愿讲解员 | 正 | 8 |
B.书香社区图书整理 | ||
C.学编中国结及义卖 | 正正 | 12 |
D.家风讲解员 | ||
E.校内志愿服务 | 正 一 | 6 |
合计 | 40 | 40 |
分析数据、推断结论
(2)抽样的40个样本数据(志愿服务项目的编号)的众数是 (填A﹣E的字母代号)
(3)请你任选A﹣E中的两个志愿服务项目,根据该同学的样本数据估计全年级大约有多少名同学选择这两个志愿服务项目.