��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+5��x�ύ��A��1��0����B��5��0�����㣬��D���������Ϻ�����Ϊ6�ĵ㣮��P�������������ϣ��Ҳ���A��D�����غϣ�����P��y���ƽ����������AD���ڵ�Q������Q��QF��ֱ��y�ᣬ��F�ڵ�Q���Ҳ࣬��QF=2����QF��QPΪ�ڱ�������QPEF�������QPEF���ܳ�Ϊd����P�ĺ�����Ϊm��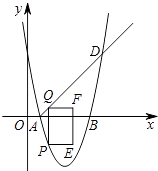
��1������������������Ӧ�ĺ�������ʽ��
��2�������������ߵĶԳ��Ὣ����QPEF�������Ϊ1��2������ʱm��ֵ��
��3����d��m֮��ĺ�����ϵʽ��d��m���������Сʱd��ȡֵ��Χ��
��4��������QPEF�ĶԽ����ഹֱʱ��ֱ��д����Գ����ĵĺ����꣮
���𰸡�
��1��
�⣺��A��1��0����B��5��0������y=ax2+bx+5��
![]() ��
��
��� ![]() ��
��
��y=x2��6x+5
��2��
�⣺��ͼ��ʾ����������y=x2��6x+5�ĶԳ���Ϊ��x=�� ![]() =��
=�� ![]() =3��
=3��
�����������ߵĶԳ��Ὣ����QPEF�������Ϊ1��2�����֣�
�ɵ�PN=3��m��PE=2��
�� ![]() =
= ![]() ��
�� ![]() =
= ![]() ��
��
��ã�m= ![]() ��m=
��m= ![]()

��3��
�⣺��x=6ʱ��y=x2��6x+5=62��6��6+5=5��
���D��������6��5����
����AD����Ӧ�ĺ�������ʽΪy=x��1��x��1����
��P��m��m2��6m+5����Q��m��m��1����
��1��m��6ʱ��d=2����m2+7m��6+2��=��2m2+14m��8��
��m��6ʱ��d=2��m2��7m+6+2��=2m2��14m+16��
��d=��2m2+14m��8=��2��m�� ![]() ��2+
��2+ ![]() ��
��
��d��m���������Сʱd��ȡֵ��Χ��4��d�� ![]()
��4��
�⣺������QPEF�ĶԽ����ഹֱʱ�������QPEF�������Σ��߳�Ϊ2��
��1��m��6ʱ��m��1����m2��6m+5��=2��
�����ã�m2��7m+8=0��
��ã�m1= ![]() ��m2=
��m2= ![]() ��
��
��m��6ʱ��m2��6m+5����m��1��=2��
�����ã�m2��7m+4=0��
��ã�m3= ![]() ��m4=
��m4= ![]() ����ȥ����
����ȥ����
����Գ����ĵĺ�����Ϊ�� ![]() +1=
+1= ![]() ��
�� ![]() +1=
+1= ![]() ��
�� ![]() +1=
+1= ![]()
����������1��ֱ�����ô���ϵ����������κ�������ʽ���ɣ���2��������������Գ�������ó�m��ֵ����3���ֱ����õ�1��m��6ʱ��d=2����m2+7m��6+2������m��6ʱ��d=2��m2��7m+6+2�����d��ȡֵ��Χ���ɣ���4��������QPEF�ĶԽ����ഹֱʱ�������QPEF�������Σ��߳�Ϊ2�������ó�m��ֵ����𰸣�
�����㾫�������ն��κ����������ǽ����ĸ�������Ҫ֪�������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��ʢʢͬѧ��ij��У����ʱ�������˶������������еIJ�����Ϣ�����±�����
Ժϵ�������ɼ����� | |||
�������� | ʤ�� | ���� | ���� |
22 | 12 | 10 | 34 |
22 | 14 | 8 | 36 |
22 | 0 | 22 | 22 |
ʢʢͬѧ���ѧϰ��֪ʶ������������⣬�����æ����������⣺
��1���ӱ��п��Կ�������һ����______��,ʤһ����_______����
��2��ij���ڱ���22����ǰ���£�ʤ���ܻ����ܵ����为���ܻ��ֵ�2������˵������.