题目内容
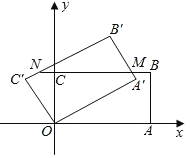
【题目】如图,平面直角坐标系中,矩形OABC绕原点O逆时针旋转30°后得到矩形OA′B′C′,A′B′与BC交于点M,延长BC交B′C′于N,若A(![]() ,0),C(0,1),则点N的坐标为( )
,0),C(0,1),则点N的坐标为( )
A.(![]() ,1)B.(
,1)B.(![]() ,1)C.(
,1)C.(![]() ,1)D.(
,1)D.(![]() ,1)
,1)
【答案】B
【解析】
由旋转的性质可得C'O=CO,∠COC'=30°,由“HL”可证Rt△CON≌Rt△C'ON,可得∠NOC=∠NOC'=15°,由直角三角形的性质可得2NC![]() NC=1,可求NC的长,即可得点N坐标.
NC=1,可求NC的长,即可得点N坐标.
如图,连接ON,作∠ONE=∠NOC.
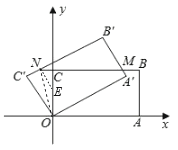
∵矩形OABC绕原点O逆时针旋转30°后得到矩形OA'B'C',
∴C'O=CO,∠COC'=30°.
∵CO=C'O,NO=NO,
∴Rt△CON≌Rt△C'ON(HL),
∴∠NOC=∠NOC'=15°,
∴∠ONE=∠NOC=15°,
∴∠NEC=30°,NE=EO.
∵NC⊥OC,∠NEO=30°,
∴NC![]() NE,CE
NE,CE![]() NC.
NC.
∵CE+OE=1,
∴2NC![]() NC=1,
NC=1,
∴NC=2![]() ,
,
∴点N坐标(2![]() ,1).
,1).
故选B.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目