题目内容
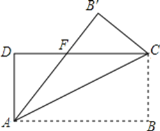
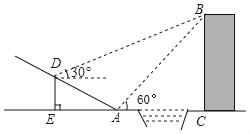
【题目】如图，某中学数学活动小组在学习了“利用三角函数测高”后，选定测量小河对岸一幢建筑物BC的高度，他们先在斜坡上的D处，测得建筑物顶端B的仰角为30°．且D离地面的高度DE=5m．坡底EA=30m，然后在A处测得建筑物顶端B的仰角是60°，点E，A，C在同一水平线上，求建筑物BC的高．（结果用含有根号的式子表示）
【答案】建筑物BC的高为
m．
【解析】分析：过点D作DH⊥BC于点H，设建筑物BC的高度为xm，则BH=（x﹣5）m，根据Rt△DHB和Rt△ACB的三角函数值得出答案．
详解：解：过点D作DH⊥BC于点H，如图所示：
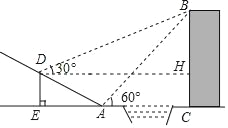
则四边形DHCE是矩形，DH=EC，DE=HC=5， 设建筑物BC的高度为xm，则BH=（x﹣5）m，
在Rt△DHB中，∠BDH=30°， ∴DH=
（x﹣5），AC=EC﹣EA=（x﹣5）﹣30，
在Rt△ACB中，∠BAC=50°，tan∠BAC=
， ∴
= 解得：x=，
答：建筑物BC的高为m．
练习册系列答案
相关题目
【题目】某商店购进一种商品，每件商品进价30元．试销中发现这种商品每天的销售量y（件）与每件销售价x（元）的关系数据如下：
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
（1）已知y与x满足一次函数关系，根据上表，求出y与x之间的关系式.（不写出自变量x的取值范围）；
（2）如果商店销售这种商品，每天要获得150元，那么每件商品的销售价应定为多少元？
（3）设该商店每天销售这种商品所获利润为w（元），求出w与x之间的关系式，并求出每件商品销售价定为多少元时利润最大？
