题目内容
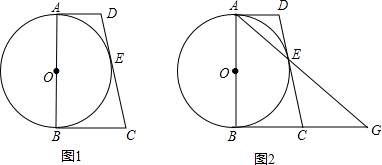
如图1,AB为⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
(1)求证:BC为⊙O的切线;
(2)连接AE,AE的延长线与BC的延长线交于点G(如图2所示),若AB=2
,AD=2,求线段BC和EG的长.
(1)求证:BC为⊙O的切线;
(2)连接AE,AE的延长线与BC的延长线交于点G(如图2所示),若AB=2
| 5 |

(1)证明:连接OE,OC;(1分)
∵CB=CE,OB=OE,OC=OC
∴△OEC≌△OBC(SSS)
∴∠OBC=∠OEC (2分)
又∵DE与⊙O相切于点E
∴∠OEC=90° (3分)
∴∠OBC=90°
∴BC为⊙O的切线.(4分)
(2)过点D作DF⊥BC于点F,
∵AD,DC,BG分别切⊙O于点A,E,B
∴DA=DE,CE=CB,
设BC为x,则CF=x-2,DC=x+2,
在Rt△DFC中,(x+2)2-(x-2)2=(2
)2,
解得:x=
;(6分)
∵AD∥BG,
∴∠DAE=∠EGC,
∵DA=DE,
∴∠DAE=∠AED;
∵∠AED=∠CEG,
∴∠EGC=∠CEG,
∴CG=CE=CB=
,(7分)
∴BG=5,
∴AG=
=
=3
;(8分)
解法一:连接BE,S△ABG=
AB•BG=
AG•BE,
∴2
×5=3
BE,
∴BE=
,(9分)
在Rt△BEG中,
EG=
=
=
,(10分)
解法二:∵∠DAE=∠EGC,∠AED=∠CEG,
∴△ADE∽△GCE,(9分)
∴
=
,
=
,
解得:EG=
.(10分)

∵CB=CE,OB=OE,OC=OC
∴△OEC≌△OBC(SSS)
∴∠OBC=∠OEC (2分)
又∵DE与⊙O相切于点E
∴∠OEC=90° (3分)
∴∠OBC=90°
∴BC为⊙O的切线.(4分)
(2)过点D作DF⊥BC于点F,
∵AD,DC,BG分别切⊙O于点A,E,B
∴DA=DE,CE=CB,
设BC为x,则CF=x-2,DC=x+2,
在Rt△DFC中,(x+2)2-(x-2)2=(2
| 5 |
解得:x=
| 5 |
| 2 |

∵AD∥BG,
∴∠DAE=∠EGC,
∵DA=DE,
∴∠DAE=∠AED;
∵∠AED=∠CEG,
∴∠EGC=∠CEG,
∴CG=CE=CB=
| 5 |
| 2 |
∴BG=5,
∴AG=
(2
|
| 45 |
| 5 |
解法一:连接BE,S△ABG=
| 1 |
| 2 |
| 1 |
| 2 |
∴2
| 5 |
| 5 |
∴BE=
| 10 |
| 3 |
在Rt△BEG中,
EG=
| BG2-BE2 |
52-(
|
| 5 |
| 3 |
| 5 |
解法二:∵∠DAE=∠EGC,∠AED=∠CEG,
∴△ADE∽△GCE,(9分)
∴
| AD |
| CG |
| AE |
| EG |
| 2 |
| 2.5 |
3
| ||
| EG |
解得:EG=
5
| ||
| 3 |


练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目



 写推理过程)写出五条结论即可.
写推理过程)写出五条结论即可.
