题目内容
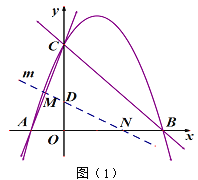
【题目】(1)观察推理:如图1,△ABC中,∠ACB=90°,AC=BC,直线l过点C,点A、B在直线l同侧,BD⊥l,AE⊥l,垂足分别为D、E.
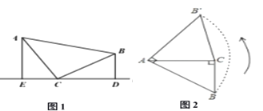
求证:△AEC≌△CDB;
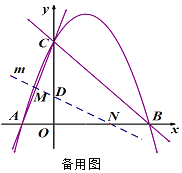
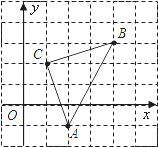
(2)类比探究:如图2,Rt△ABC中,∠ACB=90°,AC=6,将斜边AB绕点A逆时针旋转90°至AB,连接B,C,求△AB,C的面积.
【答案】(1)见详解;(2)18
【解析】
(1)利用同角的余角相等判断出∠CAE=∠BCD,即可得出结论;
(2)先作出高,进而判断出△ABC≌△B'AG,求出B'G,最后用三角形的面积公式即可得出结论.
解:(1)∵BD⊥l,AE⊥l,
∴∠AEC=∠CDB=90°,
∴∠CAE+∠ACE=90°,
∵∠ACB=90°,
∴∠ACE+∠BCD=90°,
∴∠CAE=∠BCD,
在△ACE和△CBD中,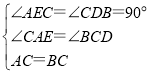
∴△ACE≌△CBD;
(2)如图2,
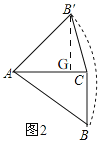
过点B'作B'G⊥AC于G,
∴∠B'AG+∠AB'G=90°,
∵∠BAB'=90°,
∴∠BAC+∠B'AG=90°,
∴∠AB'G=∠BAC,由旋转知,AB=AB',
在△ABC和△B'AG中,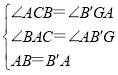
∴△ABC≌△B′AG,
∴B′G=AC=6,
∴S△ACB′=![]() AC×B′G=18;
AC×B′G=18;

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目