题目内容
【题目】直线![]() 与x轴、y轴分别交于点B、C,抛物线
与x轴、y轴分别交于点B、C,抛物线![]() 经过点B、C,并与x轴交于另一点A.
经过点B、C,并与x轴交于另一点A.
(1)求此抛物线及直线AC的函数表达式;
(2)垂直于y轴的直线l与抛物线交于点P(![]() ,
,![]() ),Q(
),Q(![]() ,
,![]() ),与直线BC交于点,N(
),与直线BC交于点,N(![]() ,
,![]() ),若
),若![]() <
<![]() <
<![]() ,结合函数的图象,求
,结合函数的图象,求![]() 的取值范围;
的取值范围;
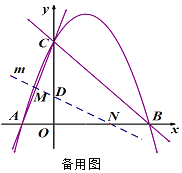
(3)经过点D(0,1)的直线m与射线AC、射线OB分别交于点M、N.当直线m绕点D旋转时,![]() 是否为定值,若是,求出这个值,若不是,说明理由.
是否为定值,若是,求出这个值,若不是,说明理由.
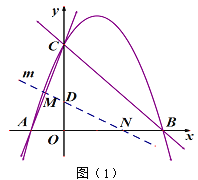
【答案】(1)=![]() ;
; ![]() ;(2)1<
;(2)1<![]() <2;(3)
<2;(3)![]() 为定值3.
为定值3.
【解析】(1)先求得直线y=-x+3与x轴、y轴的交点B、C的坐标,代入入![]() 求得a、k的值,即可得抛物线的函数表达式;令y=0,求得点A的坐标,再用待定系数法求得直线AC的函数表达式即可;(2)根据题意可得y1=y2,即可得x1+x2=2;当直线l1经过点C时,x1=x3=0,x2=2,此时x1+x3+x2=2,当直线l2经过顶点(1,4)时,直线BC的解析式为
求得a、k的值,即可得抛物线的函数表达式;令y=0,求得点A的坐标,再用待定系数法求得直线AC的函数表达式即可;(2)根据题意可得y1=y2,即可得x1+x2=2;当直线l1经过点C时,x1=x3=0,x2=2,此时x1+x3+x2=2,当直线l2经过顶点(1,4)时,直线BC的解析式为![]() ,y=4时,x=﹣1, 此时,x1=x2=1,x3=﹣1,此时x1+x3+x2=1;当直线l在直线l1与直线l2之间时,x3<x1<x2,即可得1<
,y=4时,x=﹣1, 此时,x1=x2=1,x3=﹣1,此时x1+x3+x2=1;当直线l在直线l1与直线l2之间时,x3<x1<x2,即可得1<![]() <2;(3)
<2;(3)![]() 为定值3,设直线MN的解析式为y=kx+1.把y=0代入y=kx+1得:kx+1=0,解得:x=
为定值3,设直线MN的解析式为y=kx+1.把y=0代入y=kx+1得:kx+1=0,解得:x=![]() ,所以点N的坐标为(
,所以点N的坐标为(![]() ,0).所以AN=
,0).所以AN=![]() +1=
+1=![]() 即可得
即可得![]() =
=![]() ;将y=3x+3与y=kx+1联立解得:x=
;将y=3x+3与y=kx+1联立解得:x=![]() .求得点M的横坐标为
.求得点M的横坐标为![]() . 过点M作MG⊥x轴,垂足为G.则AG=
. 过点M作MG⊥x轴,垂足为G.则AG=![]() =
=![]() .再由△MAG∽△CAO,根据相似三角形的性质可得
.再由△MAG∽△CAO,根据相似三角形的性质可得![]() ,
,![]() ,
,![]() =
=![]() =
=![]() ,由此可得
,由此可得![]() =
=![]() +
+![]() =
=![]() =3.
=3.
(1)∵直线y=-x+3与x轴、y轴分别交于点B、C,
∴B(3,0),C(0,3);
把B(3,0),C(0,3)代入![]() 得,
得,
![]() ,
,
解得![]() ,
,
∴抛物线函数表达式为![]() =
=![]() ;
;
令y=0,可得![]() =0,解得x1=-1,x2=3;
=0,解得x1=-1,x2=3;
∴A(-1,0);
设AC的解析式为y=kx+b,
![]() ,
,
解得![]() ,
,
∴直线AC的函数表达式为![]() ;
;
(2)∵y1=y2,∴x1+x2=2.
当直线l1经过点C时,x1=x3=0,x2=2,此时x1+x3+x2=2,
当直线l2经过顶点(1,4)时,直线BC的解析式为![]() ,y=4时,x=﹣1, 此时,x1=x2=1,x3=﹣1,此时x1+x3+x2=1;当直线l在直线l1与直线l2之间时,x3<x1<x2 ,
,y=4时,x=﹣1, 此时,x1=x2=1,x3=﹣1,此时x1+x3+x2=1;当直线l在直线l1与直线l2之间时,x3<x1<x2 ,
∴1<![]() <2.
<2.
(3)![]() 为定值3.
为定值3.
理由如下:设直线MN的解析式为y=kx+1.把y=0代入y=kx+1得:kx+1=0,解得:x=![]() ,
,
∴点N的坐标为(![]() ,0).∴AN=
,0).∴AN=![]() +1=
+1=![]() ,
,![]() =
=![]() ;
;
将y=3x+3与y=kx+1联立解得:x=![]() .∴点M的横坐标为
.∴点M的横坐标为![]() .
.
过点M作MG⊥x轴,垂足为G.则AG=![]() =
=![]() .
.
∵△MAG∽△CAO,∴![]() ,
,
∴![]() ,
,![]() =
=![]() =
=![]()
∴![]() =
=![]() +
+![]() =
=![]() =3.
=3.

【题目】张老师元旦节期间到武商众圆商场购买一台某品牌笔记本电脑,恰逢商场正推出“迎元旦”促销打折活动,具体优惠情况如表:
购物总金额(原价) | 折扣 |
不超过5000元的部分 | 九折 |
超过5000元且不超过10000元的部分 | 八折 |
超过10000元且不超过20000元的部分 | 七折 |
…… | …… |
例如:若购买的商品原价为15000元,实际付款金额为:
5000×90%+(10000﹣5000)×80%+(15000﹣10000)×70%=12000元.
(1)若这种品牌电脑的原价为8000元/台,请求出张老师实际付款金额;
(2)已知张老师购买一台该品牌电脑实际付费5700元.
①求该品牌电脑的原价是多少元/台?
②若售出这台电脑商场仍可获利14%,求这种品牌电脑的进价为多少元/台?