题目内容
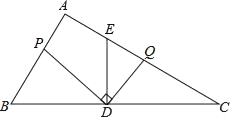
【题目】如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21.动点P从点D出发,沿射线DA的方向以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).当t为__________ 时,以B,P,Q三点为顶点的三角形是等腰三角形?

【答案】![]() 或
或![]()
【解析】
(1)由题知QB=16-t,AP=21-2t,以B、P、Q为顶点的三角形是等腰三角形,分三种情况,①PQ=BQ,②BP=PQ,③PB=BQ分别求出t即可.
如图所示,作PM⊥BC,
由题知QB=16-t,AP=21-2t,
若以B,P,Q三点为顶点的三角形是等腰三角形,可以分三种情况:
①若PQ=BQ,在Rt△PMQ中,PQ2=t2+122,
由PQ2=BQ2,得t2+122=(16﹣t)2,解得t=![]() ;
;
②若PB=PQ,由PB2=PQ2,得(16﹣2t)2+122=t2+122,
整理,得3t2﹣64t+256=0,
解得,t1=![]() ,t2=16(不合题意,舍去),
,t2=16(不合题意,舍去),
③若BP=BQ,在Rt△PMB中,BP2=(16﹣2t)2+122,
由BP2=BQ2,得(16﹣2t)2+122=(16﹣t)2,即3t2﹣32t+144=0,
∵△=﹣704<0,∴3t2﹣32t+144=0无解,
∴BP≠BQ;
综合上面的讨论可知:当t=![]() 或
或![]() 时,以B,P,Q三点为顶点的三角形是等腰三角形.
时,以B,P,Q三点为顶点的三角形是等腰三角形.


练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目