题目内容
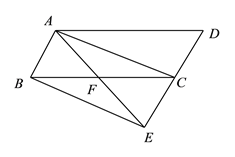
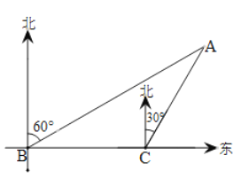
【题目】夏季是垂钓的好季节．一天甲、乙两人到松花江的
处钓鱼，突然发现在
处有一人不慎落入江中呼喊救命．如图，在处测得处在的北偏东
方向，紧急关头，甲、乙二人准备马上救人，只见甲马上从处跳水游向处救人；此时乙从沿岸边往正东方向奔跑40米到达
处，再从处下水游向处救人，已知处在的北偏东
方向上，且甲、乙二人在水中游进的速度均为1米/秒，乙在岸边上奔跑的速度为8米/秒．（注：水速忽略不计）
（1）求
、
的长．
（2）试问甲、乙二人谁能先救到人，请通过计算说明理由．（
）
【答案】（1）
米，
米，（2）乙先到达救人地点．
【解析】
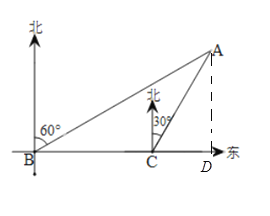
（1）过点A作AD⊥CD于点D，分别在Rt△ABD、Rt△ACD中用式子表示
再利用锐角三角函数列方程，解方程即可．
（2）分别计算出甲乙到达落水点的时间即可得到答案．
解（1）；过点A作AD⊥CD于点D，由题意得：
设
则
（2）
乙在水中所花时间为：
乙到达的时间为：
甲到达的时间为：
乙先到达救人地点．
练习册系列答案
名校名卷单元同步训练测试题系列答案
相关题目
【题目】小明同学以“你最喜欢的运动项目”为主题，对公园里参加运动的群众进行随机调查（每名被调查者只能选一个项目，且被调查者都进行了选择）.下面是小明根据调查结果列出的统计表和绘制的扇形统计图（不完整）.
被调查者男、女所选项目人数统计表
项目 | 男（人数） | 女（人数） |
广场舞 | 7 | 9 |
健步走 |
| 4 |
器械 | 2 | 2 |
跑步 | 5 |
|
根据以上信息回答下列问题：
（1）统计表中的
__________，
__________.
（2）扇形统计图中“广场舞”项目所对应扇形的圆心角度数为__________°.
（3）若平均每天来该公园运动的人数有3600人，请你估计这3600人中最喜欢的运动项目是“跑步”的约有多少人？
