题目内容
如图，点A、B在直线MN上，AB=8cm，⊙A、⊙B的半径均为1cm．⊙A以每秒1cm的速度自左向右运动；与此同时，⊙B的半径也随之增大，其半径r（cm）与时间t（秒）之间满足关系式r=1+t（t≥0）．则当点A出发后考点：圆与圆的位置关系
专题：动点型
分析：根据两圆相切时，两圆的半径与圆心距的关系，注意有4种情况．
解答：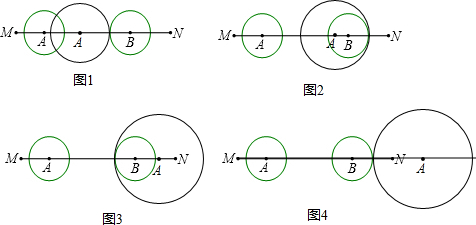
解：分四种情况考虑：
①当首次外切时，有t+1+1+t=8，解得：t=3；
②当首次内切时，有t+1+t-1=8，解得：t=4；
③当再次内切时，有t-（1+t-1）=8，t无解；
④当再次外切时，有t-（1+t）-1=8，无解．
∴当点A出发后3、4秒两圆相切，
故答案为：3或4．
解：分四种情况考虑：①当首次外切时，有t+1+1+t=8，解得：t=3；
②当首次内切时，有t+1+t-1=8，解得：t=4；
③当再次内切时，有t-（1+t-1）=8，t无解；
④当再次外切时，有t-（1+t）-1=8，无解．
∴当点A出发后3、4秒两圆相切，
故答案为：3或4．
点评：本题考查了两圆相切时，两圆的半径与圆心距的关系，注意有4种情况．
练习册系列答案
相关题目
如图，∠AOC=∠BOC，点P在OC上，PD⊥OA，PE⊥OB，垂足分别为D、E，则△PDO≌△PEO的依据是（ ）| A、SSS | B、SAS |
| C、AAS | D、HL |
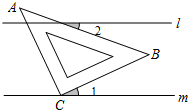如图，直线l∥m，将含有45°角的三角板ABC的直角顶点C放在直线m上，则
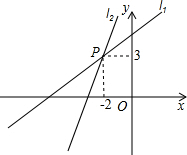如图，一次函数y=kx1+b1的图象l1与y=kx2+b2的图象l2相交于点P，则方程组
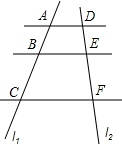如图，已知AD∥BE∥CF，它们依次交直线l1、l2于点A、B、C和点D、E、F，如果DE：EF=3：5，AC=24，则BC=
已知图中的两个三角形全等，则∠1等于（ ）| A、72° | B、60° |
| C、50° | D、58° |
以下四条直线中，与直线y=2x+3相交于第一象限的是（ ）
| A、直线y=2x-4 |
| B、直线y=-x+3 |
| C、直线y=-3x+2 |
| D、直线y=x+4 |