题目内容
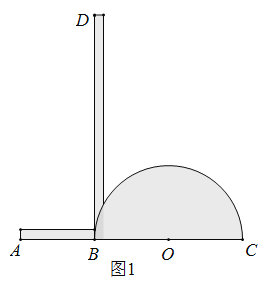
【题目】我们学习过利用用尺规作图平分一个任意角,而“利用尺规作图三等分一个任意角”曾是数学史上一大难题,之后被数学家证明是不可能完成的,人们根据实际需要,发明了一种简易操作工具--------三分角器.图1是它的示意图,其中![]() 与半圆
与半圆![]() 的直径
的直径![]() 在同一直线 上,且
在同一直线 上,且![]() 的长度与半圆的半径相等;
的长度与半圆的半径相等;![]() 与
与![]() 重直于点
重直于点 ![]() 足够长.
足够长.
使用方法如图2所示,若要把![]() 三等分,只需适当放置三分角器,使
三等分,只需适当放置三分角器,使![]() 经过
经过![]() 的顶点
的顶点![]() ,点
,点![]() 落在边
落在边![]() 上,半圆
上,半圆![]() 与另一边
与另一边![]() 恰好相切,切点为
恰好相切,切点为![]() ,则
,则![]() 就把
就把![]() 三等分了.
三等分了.
为了说明这一方法的正确性,需要对其进行证明.如下给出了不完整的“已知”和“求证”,请补充完整,并写出“证明”过程.
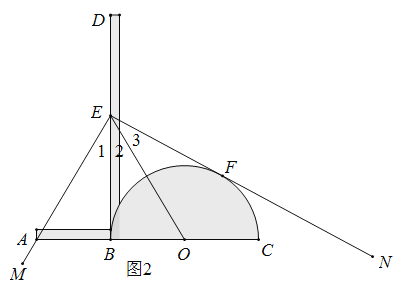
已知:如图2,点在![]() 同一直线上,
同一直线上,![]() 垂足为点
垂足为点![]() ,
,
求证:
【答案】![]() 在
在![]() 上,
上,![]() 过点
过点![]() ,
,![]()
![]() 为半圆
为半圆![]() 的切线,切点为
的切线,切点为![]() ;EB,EO为∠MEN的三等分线.证明见解析.
;EB,EO为∠MEN的三等分线.证明见解析.
【解析】
如图,连接OF.则∠OFE=90°,只要证明![]() ,
,![]() ,即可解决问题;
,即可解决问题;
已知:如图2,点在![]() 同一直线上,
同一直线上,![]() 垂足为点
垂足为点![]() ,
, ![]() 在
在![]() 上,
上,![]() 过点
过点![]() ,
,![]()
![]() 为半圆
为半圆![]() 的切线,切点为
的切线,切点为![]() .
.
求证: EB,EO为∠MEN的三等分线.
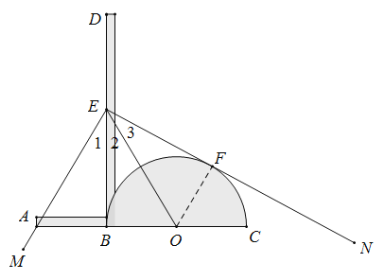
证明:如图,连接OF.则∠OFE=90°,
∵EB⊥AC,EB与半圆相切于点B,
∴∠ABE=∠OBE=90°,
∵BA=BO.EB=EB,
![]()
∴∠AEB=∠BEO,
∵EO=EO.OB=OF,∠OBE=∠OFE![]() ,
,
∴![]() ,
,
∴∠OEB=∠OEF,
∴∠AEB=∠BEO=∠OEF,
∴EB,EO为∠MEN的三等分线.
故答案为:![]() 在
在![]() 上,
上,![]() 过点
过点![]() ,
,![]()
![]() 为半圆
为半圆![]() 的切线,切点为
的切线,切点为![]() .
.
EB,EO为∠MEN的三等分线.

 名校课堂系列答案
名校课堂系列答案【题目】(2017陕西)养成良好的早锻炼习惯,对学生的学习和生活都非常有益.某中学为了了解七年级学生的早锻炼情况,校政教处在七年级随机抽取了部分学生,并对这些学生通常情况下一天的早锻炼时间![]() (分钟)进行了调查.现把调查结果分成
(分钟)进行了调查.现把调查结果分成![]() 四组,如下表所示;同时,将调查结果绘制成下面两幅不完整的统计图.
四组,如下表所示;同时,将调查结果绘制成下面两幅不完整的统计图.
组别 | 时间 |
|
|
|
|
|
|
|
|
所抽取七年级学生早锻炼时间统计图
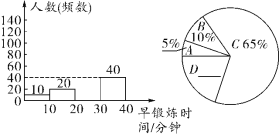
请你根据以上提供的信息,解答下列问题:
(1)补全频数分布直方图和扇形统计图;
(2)所抽取的七年级学生早锻炼时间的中位数落在________区间内;
(3)已知该校七年级共有1200名学生,请你估计这个年级学生中约有多少人一天早锻炼的时间不少于20分钟.(早锻炼:指学生在早晨7:00~7:40之间的锻炼)
【题目】某垃圾处理厂,只能处理![]() 、
、![]() 两类垃圾,且每天只能处理其中的一类垃圾,已知该垃圾厂每月工作25天,每天处理垃圾种类的吨数及费用如下表:
两类垃圾,且每天只能处理其中的一类垃圾,已知该垃圾厂每月工作25天,每天处理垃圾种类的吨数及费用如下表:
|
| |
每天处理的吨数(单位:吨) | 22 | 30 |
每吨处理的费用(单位:元) | 150 | 100 |
设该垃圾厂每月处理![]() 类垃圾
类垃圾![]() 天,这个厂每月处理垃圾的总吨数为
天,这个厂每月处理垃圾的总吨数为![]() 吨,每月处理垃圾所需的总费用为
吨,每月处理垃圾所需的总费用为![]() 元,据测算该厂每月最多处理垃圾590吨.
元,据测算该厂每月最多处理垃圾590吨.
(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)![]() 为何值时,
为何值时,![]() 最小,最小值是多少?
最小,最小值是多少?
(3)一段时间后,由于改进了处理![]() 类垃圾的流程,使处理每吨
类垃圾的流程,使处理每吨![]() 类垃圾的费用减少了
类垃圾的费用减少了![]() 元(
元(![]() ),
),![]() 类垃圾的处理费用没有改变,求该厂每月处理垃圾费用最少时,处理
类垃圾的处理费用没有改变,求该厂每月处理垃圾费用最少时,处理![]() 、
、![]() 两类垃圾的天数各是多少?
两类垃圾的天数各是多少?