题目内容
【题目】某垃圾处理厂，只能处理
、
两类垃圾，且每天只能处理其中的一类垃圾，已知该垃圾厂每月工作25天，每天处理垃圾种类的吨数及费用如下表：
|
| |
每天处理的吨数（单位：吨） | 22 | 30 |
每吨处理的费用（单位：元） | 150 | 100 |
设该垃圾厂每月处理类垃圾
天，这个厂每月处理垃圾的总吨数为
吨，每月处理垃圾所需的总费用为
元，据测算该厂每月最多处理垃圾590吨．
（1）求与的函数关系式；
（2）为何值时，最小，最小值是多少？
（3）一段时间后，由于改进了处理类垃圾的流程，使处理每吨类垃圾的费用减少了
元（
），类垃圾的处理费用没有改变，求该厂每月处理垃圾费用最少时，处理、两类垃圾的天数各是多少？
【答案】（1）
；（2）每月处理A类垃圾20天时，总费用最小，最小为81000元；（3）处理A类垃圾20天，B类垃圾5天时，这时处理垃圾总费用最少；处理A类垃圾天数在
间的整数天时，处理垃圾总费用都一样；处理A类垃圾25天，不处理B类垃圾时，处理垃圾总费用最少
【解析】
解：（1）由题意得，
；
（2）由于该厂每月最多处理590吨，所以
，
解得
，
由题意得：
，
∵
，
∴w随x增大而增大，
∵
，
∴，
∴当
时，w最小，最小为
，
∴每月处理A类垃圾20天时，总费用最小，最小为81000元；
（3）由题意得，
，其中，
①∵当
时，
，w随x的增大而增大，
∴当时，w有最小值．
即处理A类垃圾20天，B类垃圾5天时，这时处理垃圾总费用最少；
②∵当
时，
，
，
即处理A类垃圾天数在间的整数天时，处理垃圾总费用都一样；
③∵当
时，
，w随x的增大而减小，
∴当
时，w有最小值，
即处理A类垃圾25天，不处理B类垃圾时，处理垃圾总费用最少．
练习册系列答案
相关题目
【题目】在春季运动会上，某学校教工组和学生组进行定点投篮比赛，每组均派五名选手参加，每名选手投篮十次，投中记1分，不中记零分，3分以上(含3分)视为合格，比赛成绩绘制成条形统计图如下：
投篮成绩条形统计图
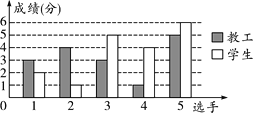
(1)请你根据条形统计图中的数据填写表格：
组别 | 平均数 | 中位数 | 方差 | 合格率 |
教工组 | ________ | 3 | ________ | 80% |
学生组 | 3.6 | ________ | 3.44 | 60% |
(2)如果小亮认为教工组的成绩优于学生组，你认为他的理由是什么？小明认为学生组成绩优于教工组，他的理由又是什么？
(3)若再让一名体育教师投篮后，六名教师成绩平均数大于学生组成绩的中位数，设这名体育教师命中m分，求m的值．
