[题目]如图.△ABC中.若AC=4.BC=3.AB=5.则△ABC的内切圆半径R= ．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，△ABC中，若AC=4，BC=3，AB=5，则△ABC的内切圆半径R=_____．

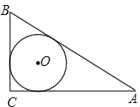
【答案】1．

【解析】

先根据已知条件得出△ABC为直角三角形，再根据三角形的面积公式计算出△ABC的面积，再连接AO,BO,CO，S△ABC=S△AOB+S△BOC+S△AOC，设内切圆半径为r，再根据面积公式计算即可得出结论.

∵AB=5，AC=4，BC=3，32+42=52，

∴AB2=AC2+BC2，

∴△ABC为直角三角形,

∴S△ABC=×AC×BC=×4×3=6，

设△ABC的内切圆圆心为O，连接AO,BO,CO，

∴S△ABC=S△AOB+S△BOC+S△AOC，

设内切圆半径为r，则ABr+BCr+ACr=6，

5r+3r+4r=6，

解得r=1.

故答案为1.

练习册系列答案

考必胜小学毕业升学考试试卷精选系列答案

A．线段DB绕点D顺时针旋转一定能与线段DC重合

B．线段DB绕点D顺时针旋转一定能与线段DI熏合

C．∠CAD绕点A顺时针旋转一定能与∠DAB重合

D．线段ID绕点I顺时针旋转一定能与线段IB重合

【题目】已知点P在一次函数y=kx+b（k，b为常数，且k＜0，b＞0）的图象上，将点P向左平移1个单位，再向上平移2个单位得到点Q，点Q也在该函数y=kx+b的图象上．

（1）k的值是；

（2）如图，该一次函数的图象分别与x轴、y轴交于A，B两点，且与反比例函数y=图象交于C，D两点（点C在第二象限内），过点C作CE⊥x轴于点E，记S1为四边形CEOB的面积，S2为△OAB的面积，若=，则b的值是．

【题目】如图，AB是⊙O的直径，C，D是⊙O上的点，且OC∥BD，AD分别与BC，OC相交于点E，F，则下列结论：①AD⊥BD；②∠AOC=∠AEC；③CB平分∠ABD；④AF=DF；⑤BD=2OF；⑥△CEF≌△BED，其中一定成立的____（把你认为正确结论的序号都填上）

【题目】如图，AB为⊙O的直径，CD切⊙O于点C，与BA的延长线交于点D，OE⊥AB交⊙O于点E，连接CA、CE、CB，CE交AB于点G，过点A作AF⊥CE于点F，延长AF交BC于点P．

（Ⅰ）求∠CPA的度数；

（Ⅱ）连接OF，若AC=，∠D=30°，求线段OF的长．

【题目】如图，一段圆弧与长度为1的正方形网格的交点是A、B、C．

(1)请完成以下操作：

①以点O为原点，垂直和水平方向为轴，网格边长为单位长，建立平面直角坐标系；

②根据图形提供的信息，标出该圆弧所在圆的圆心D，并连接AD、CD；

(2)请在(1)的基础上，完成下列填空：⊙D的半径为__________；点（6，–2）在⊙D__________；（填“上”、“内”、“外”）∠ADC的度数为__________．

【题目】如图，AB是半圆O的直径，点D是半圆O上一点，点C是的中点，CE⊥AB于点E，过点D的切线交EC的延长线于点G，连接AD，分别交CE、CB于点P、Q，连接AC．

（1）求证：GP＝GD；

（2）求证：P是线段AQ的中点；

（3）连接CD，若CD＝2，BC＝4，求⊙O的半径和CE的长．

【题目】李刚和常明两人在数学活动课上进行折纸创编活动.李刚拿起一张准备好的长方形纸片对常明说:“我现在折叠纸片（图①），使点D落在AB边的点F处，得折痕AE，再折叠，使点C落在AE边的点G处，此时折痕恰好经过点B，如果AD=，那么AB长是多少？”常明说；“简单，我会. AB应该是_____”.

常明回答完，又对李刚说：“你看我的创编（图②），与你一样折叠，可是第二次折叠时，折痕不经过点B，而是经过了AB边上的M点，如果AD=，测得EC=3BM，那么AB长是多少？”李刚思考了一会，有点为难，聪明的你，你能帮忙解答吗？AB=_____.

【题目】如图，建筑物AB的高为6cm，在其正东方向有个通信塔CD，在它们之间的地面点M（B，M，D三点在一条直线上）处测得建筑物顶端A、塔项C的仰角分别为37°和60°，在A处测得塔顶C的仰角为30°，则通信塔CD的高度．（sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，=1.73，精确到0.1m）

试题分类