题目内容
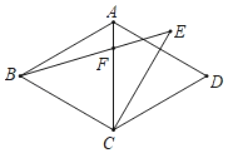
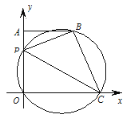
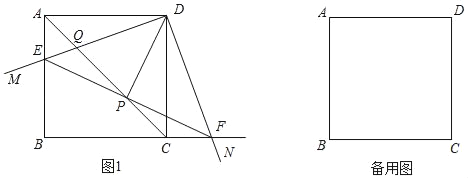
【题目】如图,在正方形ABCD中,边长为4,∠MDN=90°,将∠MDN绕点D旋转,其中DM边分别与射线BA、直线AC交于E、Q两点,DN边与射线BC交于点F;连接EF,且EF与直线AC交于点P.
(1)如图1,点E在线段AB上时,①求证:AE=CF;②求证:DP垂直平分EF;
(2)当AE=1时,求PQ的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)①只要证明△ADE≌△CDE(ASA)即可解决问题;
②利用相似三角形的性质证明∠PDQ=45°即可解决问题;
(2)作QH⊥AD于H,QE⊥AB于G.由△AQD∽△EQP,可知AQPQ=DQEQ,想办法求出AQ,EQ,DQ即可解决问题;
(1)①证明:∵四边形ABCD是正方形,
∴DA=DC,∠ADC=∠DAE=∠DCF=90°,
∴∠ADC=∠MDN=90°,
∴∠ADE=∠CDF,
∴△ADE≌△CDE(ASA),
∴AE=CF.
②∵△ADE≌△CDE(ASA),
∴DE=DF,∵∠MDN=90°,
∴∠DEF=45°,
∵∠DAC=45°,
∴∠DAQ=∠PEQ,∵∠AQD=∠EQP,
∴△AQD∽△EQP,
∴![]() ,
,
∴![]() ,
,
∵∠AQE=∠PQD,
∴△AQE∽△DQP,
∴∠DDP=∠QAE=45°,
∴∠DPE=90°,
∴DP⊥EF,
∵DE=DF,
∴PE=PF,
∴DP垂直平分线段EF.
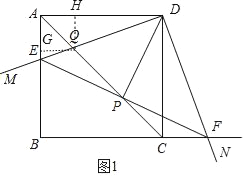
(2)解:作QH⊥AD于H,QE⊥AB于G.
在Rt△ADE中,DE=![]() ,
,
∵∠QAH=∠QAG=45°,
∴HO=QE=AH=EQ,设QH=x,
∵![]() ×4×x+
×4×x+![]() ×1×x=
×1×x=![]() ×1×4,
×1×4,
∵x=![]() ,
,
∴AQ=![]() ,DQ=
,DQ=![]() =
=![]() ,EQ=
,EQ=![]() ,
,
∵△AQD∽△EQP,
∴AQPQ=DQEQ,
∴PQ=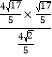 =
=![]() .
.

练习册系列答案
相关题目