题目内容
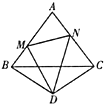
【题目】如图,在菱形ABCD中,∠BAD=120°,CE⊥AD,且CE=BC,连接BE交对角线AC于点F,则∠EFC=_____°.
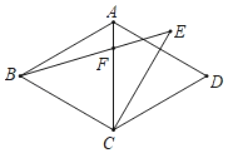
【答案】105°
【解析】
由菱形及菱形一个内角为120°,可得△ABC与△ACD为等边三角形.CE⊥AD可由三线合一得CE平分∠ACD,即求得∠ACE的度数.再由CE=BC可求出∠E的度数,根据三角形内角和即可得∠EFC的度数.
解:∵菱形ABCD中,∠BAD=120°
∴AB=BC=CD=AD,∠BCD=120°,∠ACB=∠ACD=![]() ∠BCD=60°,
∠BCD=60°,
∴△ACD是等边三角形
∵CE⊥AD
∴∠ACE=![]() ∠ACD=30°
∠ACD=30°
∴∠BCE=∠ACB+∠ACE=90°
∵CE=BC
∴∠E=∠CBE=45°
∴∠EFC=180°﹣∠E﹣∠ACE=180°﹣45°﹣30°=105°
故答案为:105°

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
【题目】某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,然后再按笔试占![]() 、面试占
、面试占![]() 计算候选人的综合成绩.他们的各项成绩如下表所示:
计算候选人的综合成绩.他们的各项成绩如下表所示:
候选人 | 笔试成绩/分 | 面试成绩/分 |
甲 |
|
|
乙 |
|
|
丙 |
|
|
丁 |
|
|
(1)现得知候选人丙的综合成绩为![]() 分,求表中
分,求表中![]() 的值
的值
(2)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
【题目】探究函数![]() 的图象与性质.
的图象与性质.
小王根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小亮的探究过程,请你帮忙补充完整:
(1)下表是![]() 与
与![]() 的几组对应值
的几组对应值
| … |
|
|
|
|
|
|
|
|
| … |
| … |
|
|
|
|
|
|
|
|
| … |
则![]() _______;
_______;![]() _______;
_______;
(2)在平面直角坐标系![]() 中,描出以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象:
中,描出以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象:
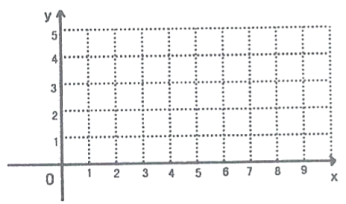
(3)结合函数图象,解决问题:当![]() 时,直接写出所有满足条件的
时,直接写出所有满足条件的![]() 的近似值(精确到
的近似值(精确到![]() ).
).