题目内容
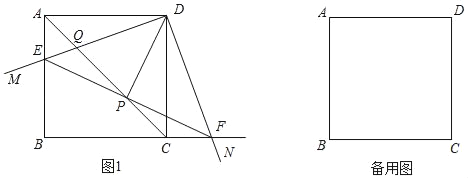
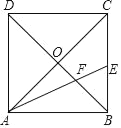
【题目】如图,正方形ABCD的边长为![]() +1,对角线AC、BD相交于点O,AE平分∠BAC分别交BC、BD于E、F,
+1,对角线AC、BD相交于点O,AE平分∠BAC分别交BC、BD于E、F,
(1)求证:△ABF∽△ACE;
(2)求tan∠BAE的值;
(3)在线段AC上找一点P,使得PE+PF最小,求出最小值.
【答案】(1)证明见解析;(2)tan∠EAB=![]() ﹣1;(3)PE+PF的最小值为
﹣1;(3)PE+PF的最小值为![]() .
.
【解析】
(1)根据两角对应相等的两个三角形相似判断即可;
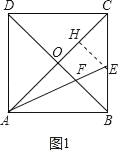
(2)如图1中,作EH⊥AC于H.首先证明BE=EH=HC,设BE=EH=HC=x,构建方程求出x即可解决问题;
(3)如图2中,作点F关于直线AC的对称点H,连接EH交AC于点P,连接PF,此时PF+PE的值最小,最小值为线段EH的长;
(1)证明:∵四边形ABCD是正方形,
∴∠ACE=∠ABF=∠CAB=45°,
∵AE平分∠CAB,
∴∠EAC=∠BAF=22.5°,
∴△ABF∽△ACE.
(2)解:如图1中,作EH⊥AC于H.
∵EA平分∠CAB,EH⊥AC,EB⊥AB,
∴BE=EB,
∵∠HCE=45°,∠CHE=90°,
∴∠HCE=∠HEC=45°,
∴HC=EH,
∴BE=EH=HC,设BE=HE=HC=x,则EC=![]() x,
x,
∵BC=![]() +1,
+1,
∴x+x=![]() +1,
+1,
∴x=1,
在Rt△ABE中,∵∠ABE=90°,
∴tan∠EAB=![]() ﹣1.
﹣1.
(3)如图2中,作点F关于直线AC的对称点H,连接EH交AC于点P,连接PF,此时PF+PE的值最小.
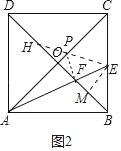
作EM⊥BD于M.BM=EM=![]() ,
,
∵AC=![]() =2+
=2+![]() ,
,
∴OA=OC=OB=![]() AC=
AC=![]() ,
,
∴OH=OF=OAtan∠OAF=OAtan∠EAB=![]() (
(![]() ﹣1)=
﹣1)=![]() ,
,
∴HM=OH+OM=![]() ,
,
在Rt△EHM中,EH=![]() =
=![]() ..
..
∴PE+PF的最小值为![]() ..
..

 口算题卡加应用题集训系列答案
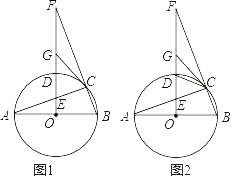
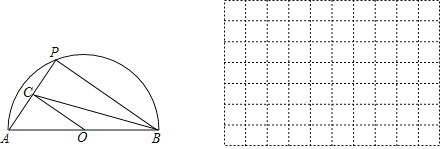
口算题卡加应用题集训系列答案【题目】如图,P是半圆弧![]() 上一动点,连接PA、PB,过圆心O作
上一动点,连接PA、PB,过圆心O作![]() 交PA于点C,连接
交PA于点C,连接![]() 已知
已知![]() ,设O,C两点间的距离为xcm,B,C两点间的距离为ycm.
,设O,C两点间的距离为xcm,B,C两点间的距离为ycm.
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行探究.
下面是小东的探究过程,请补充完整:
![]() 通过取点、画图、测量,得到了x与y的几组值,如下表:
通过取点、画图、测量,得到了x与y的几组值,如下表:
| 0 |
| 1 |
| 2 |
| 3 |
| 3 |
|
|
|
| 6 |
![]() 说明:补全表格时相关数据保留一位小数
说明:补全表格时相关数据保留一位小数![]()
![]() 建立直角坐标系,描出以补全后的表中各对应值为坐标的点,画出该函数的图象;
建立直角坐标系,描出以补全后的表中各对应值为坐标的点,画出该函数的图象;
![]() 结合画出的函数图象,解决问题:直接写出
结合画出的函数图象,解决问题:直接写出![]() 周长C的取值范围是______.
周长C的取值范围是______.
【题目】某次模拟考试后,抽取 m 名学生的数学成绩进行整理分组,形成如下表格(x 代表成绩),并绘制出扇形统计图和频数分布直方图(横坐标表示成绩,单位:分).
A 组 | 140<x≤150 |
B 组 | 130<x≤140 |
C 组 | 120<x≤130 |
D 组 | 110<x≤120 |
E 组 | 100<x≤110 |
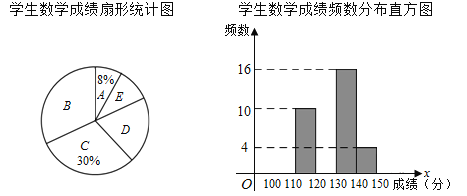
(1)m 的值为多少,扇形统计图中 D 组对应的圆心角是多少度.
(2)请补全条形统计图,并标注出相应的人数.
(3)若此次考试数学成绩 130 分以上的为优秀,参加此次模拟考的学生总数为 2000,请估算此次考试数学成绩优秀的学生人数.