Question

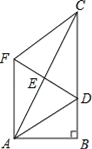
【题目】在△ABC中，AB＝AC，∠BAC＝90°，点D在射线BC上（不与点B、点C重合），将线段AD绕A逆时针旋转90°得到线段AE，作射线BA与射线CE，两射线交于点F．

（1）若点D在线段BC上，如图1，请直接写出CD与EF的关系．

（2）若点D在线段BC的延长线上，如图2，（1）中的结论还成立吗？请说明理由．

（3）在（2）的条件下，连接DE，G为DE的中点，连接GF，若tan∠AEC＝，AB＝，求GF的长．

Answer 1

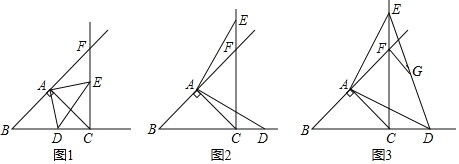
【答案】（1）CD＝EF，CD⊥EF；（2）结论仍然成立，理由见解析；（3）

【解析】

（1）由旋转的性质可得AD=AE，∠DAE=90°=∠BAC，由“SAS”可证△ABD≌△ACE，可得BD=CE，∠ABD=∠ACE=45°，可证CD⊥EF，由等腰三角形的性质可得BC=CF，可证CD=EF；

（2）由旋转的性质可得AD=AE，∠DAE=90°=∠BAC，由“SAS”可证△ABD≌△ACE，可得BD=CE，∠ABD=∠ACE=45°，可证CD⊥EF，由等腰三角形的性质可得BC=CF，可证CD=EF；

（3）过点A作AN⊥CE于点N，过点G作GH⊥CE于H，由直角三角形的性质可求BC=CF=2，AN=CN=1，锐角三角函数可求EN=2，由平行线分线段成比例可求GH，FH的长，由勾股定理可求解．

（1）CD＝EF，CD⊥EF，

理由如下：∵AB=AC，∠BAC=90°，

∴∠ABC=∠ACB=45°，

∵将线段AD绕A逆时针旋转90°得到线段AE，

∴AD=AE，∠DAE=90°=∠BAC，

∴∠BAD=∠CAE，且AB=AC，AD=AE，

∴△ABD≌△ACE（SAS）

∴BD=CE，∠ABD=∠ACE=45°，

∴∠BCF=∠ACB+∠ACE=90°，

∴CD⊥EF，

又∵∠ABC=45°，

∴∠BFC=∠ABC，

∴BC=CF，

∴CD=EF；

（2）结论仍然成立，

理由如下：∵AB＝AC，∠BAC＝90°，

∴∠ABC=∠ACB＝45°，

∵将线段AD绕A逆时针旋转90°得到线段AE，

∴AD＝AE，∠DAE＝90°＝∠BAC，

∴∠BAD＝∠CAE，且AB＝AC，AD＝AE，

∴△ABD≌△ACE（SAS）

∴BD＝CE，∠ABD＝∠ACE＝45°，

∴∠BCF＝∠ACB+∠ACE＝90°，

∴CD⊥EF，

又∵∠ABC＝45°，

∴∠BFC＝∠ABC，

∴BC＝CF，

∴CD＝EF；

（3）如图，过点A作AN⊥CE于点N，过点G作GH⊥CE于H，

∵，

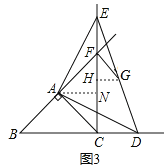
∴BC＝CF＝2，

∵AN⊥CE，∠ACF＝45°，

∴AN＝CN＝1，

∵，

∴EN＝2，

∴EC＝CN+EN＝3，

∴EF＝EC﹣CF＝1＝CD，

∵GH⊥CE，∠ECD＝90°，

∴HG∥CD，

∴ ，且EG＝DG，

∴，，

∴

∴.