题目内容
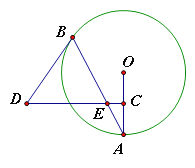
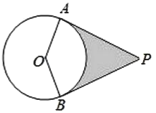
【题目】如图,![]() 的半径为4,过圆外一点
的半径为4,过圆外一点![]() 画
画![]() 的两条切线
的两条切线![]() 和
和![]() ,
,![]() 、
、![]() 为切点,若
为切点,若![]() ,则阴影部分的面积是__________.(结果保留
,则阴影部分的面积是__________.(结果保留![]() )
)
【答案】![]()
【解析】
连接OP,如图,根据切线的性质和切线长定理得到∠PAO=∠PBO=90°,∠APO=30°,则根据四边形内角和得到∠AOB=180°-∠APB=120°,再在Rt△PAO中利用含30度的直角三角形三边的关系得到![]() ,则
,则![]() ,然后根据扇形面积公式,利用阴影部分的面积=S四边形AOBP-S扇形AOB进行计算.
,然后根据扇形面积公式,利用阴影部分的面积=S四边形AOBP-S扇形AOB进行计算.
连接OP,如图,
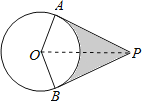
∵PA,PB是⊙O的两条切线,
∴OA⊥AP,OB⊥PB,OP平分∠APB,
∴∠PAO=∠PBO=90°, ![]() ,
,
∴∠AOB=180°-∠APB=180°-60°=120°,
在Rt△PAO中,∵OA=4,∠APO=30°,
∴![]() ,
,
∴![]() ,
,
∴阴影部分的面积![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目