题目内容
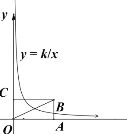
【题目】已知:如图,直线![]() 交坐标轴于A、C两点,抛物线
交坐标轴于A、C两点,抛物线![]() 过A、C两点.
过A、C两点.
(1)求抛物线的解析式;
(2)若点P为抛物线位于第三象限上一动点,连接PA,PC,试问△PAC是否存在最大值,若存在,请求出△APC取最大值以及点P的坐标,若不存在,请说明理由;
(3)点M为抛物线上一点,点N为抛物线对称轴上一点,若△NMC是以∠NMC为直角的等腰直角三角形,请直接写出点M的坐标.

【答案】(1)![]() ;(2)存在,△PAC的面积最大值为
;(2)存在,△PAC的面积最大值为![]() ,点P的坐标为(
,点P的坐标为(![]() ,
,![]() );(3)点M的坐标为:
);(3)点M的坐标为: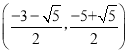 或
或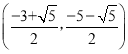 或(
或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)由一次函数解析式求得A、C两点的坐标,然后代入到二次函数解析式,用待定系数法求解;
(2)过点P作PQ⊥x轴,垂足为Q,直线PQ,AC交于点P,设点P的坐标为(![]() ,
,![]() ),则点D的坐标为(
),则点D的坐标为(![]() ,
,![]() ),根据两点间距离公式求得PD =
),根据两点间距离公式求得PD =![]() ,然后根据三角形面积公式求得
,然后根据三角形面积公式求得![]() =
=![]() =
=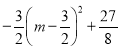 ,由此根据二次函数的性质分析最值;
,由此根据二次函数的性质分析最值;
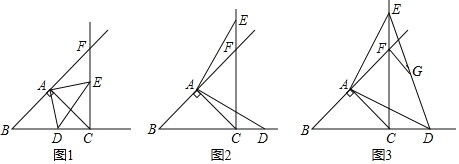
(3)分情况讨论:当点M在对称轴左侧时,构造矩形EFCG,设点M的坐标为(![]() ,
,![]() ),利用AAS定理证明△MEN≌△CFM,然后结合抛物线对称轴求得MF=
),利用AAS定理证明△MEN≌△CFM,然后结合抛物线对称轴求得MF=![]() =
=![]() ,NE=
,NE=![]() ,从而列方程求解;作MF⊥y轴,垂足为F,MF交对称轴于点E;设点M的坐标为(
,从而列方程求解;作MF⊥y轴,垂足为F,MF交对称轴于点E;设点M的坐标为(![]() ,
,![]() ),则ME=
),则ME= ![]() ,CF=
,CF= ![]() ,然后列方程求解;当点M在对称轴的右侧时,过点M作EF∥x轴,分别交对称轴与y轴于点E和点F.设点M的坐标为(
,然后列方程求解;当点M在对称轴的右侧时,过点M作EF∥x轴,分别交对称轴与y轴于点E和点F.设点M的坐标为(![]() ,
,![]() ),然后结合抛物线对称轴求得ME=
),然后结合抛物线对称轴求得ME= ![]() =
=![]() ,CF=
,CF= ![]() =
= ![]() ,然后列方程求解;作ME⊥对称轴,垂足为E,ME交NC,交点为F.设点M的坐标为(
,然后列方程求解;作ME⊥对称轴,垂足为E,ME交NC,交点为F.设点M的坐标为(![]() ,
,![]() ),则ME=
),则ME= ![]() ,CF=
,CF= ![]() ,然后列方程求解.
,然后列方程求解.
解:(1)![]() 交x轴于A(-3,0),交y轴于C(0,-3),
交x轴于A(-3,0),交y轴于C(0,-3),
∵抛物线![]() 经过点A(-3,0),点C(0,-3),
经过点A(-3,0),点C(0,-3),
∴![]() ,解得
,解得![]() ,
,
∴抛物线解析式为:![]() ;
;
(2)如图2,过点P作PQ⊥x轴,垂足为Q,直线PQ,AC交于点P,
设点P的坐标为(![]() ,
,![]() ),则点D的坐标为(
),则点D的坐标为(![]() ,
,![]() ),
),
∴线段PD的长为:(![]() )-(
)-(![]() )=
)=![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() =
=![]() =
=![]() =
=![]() =
=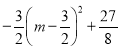 ,
,
∵![]() ,∴当
,∴当![]() 时候,△PAC的面积又最大值,最大值为
时候,△PAC的面积又最大值,最大值为![]() ,
,
此时点P的坐标为(![]() ,
,![]() );
);
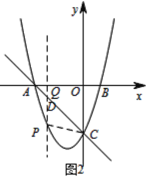
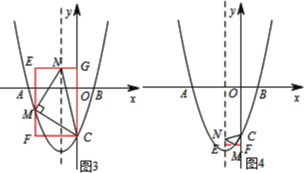
(3)①如图3,当点M在对称轴左侧时,构造矩形EFCG,设点M的坐标为(![]() ,
,![]() ),
),
∵△NMC是以∠NMC为直角的等腰直角三角形
∴∠NME+∠CMF=90°,∠FCM+∠CMF=90°
∴∠NME=∠FCM
又∵∠E=∠F=90°,MN=MC
∴△MEN≌△CFM,
∵抛物线![]() 的对称轴为直线x=-1,
的对称轴为直线x=-1,
∴MF=![]() =
=![]() ,NE=
,NE=![]() ,
,
∵MF=NE,∴![]() ,
,
解得![]() (舍),
(舍),![]() ,
,
故点M的坐标为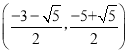 ;
;
②如图6,作MF⊥y轴,垂足为F,MF交对称轴于点E;
设点M的坐标为(![]() ,
,![]() ),则ME=
),则ME= ![]() ,CF=
,CF= ![]() ,
,
由①同理可证△MNE≌△CFM,
∵ME=CF,故![]() ,
,
解得:![]() (舍),
(舍),![]() ,
,
故点M的坐标为(![]() ,
,![]() );
);
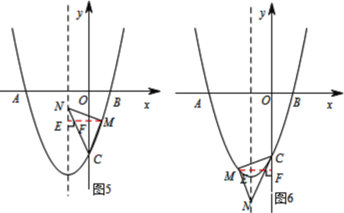
③如图5,当点M在对称轴的右侧时,过点M作EF∥x轴,分别交对称轴与y轴于点E和点F.
设点M的坐标为(![]() ,
,![]() ),
),
由①同理可证△MEN≌△MFC,抛物线对称轴为直线x=-1,
则ME= ![]() =
=![]() ,CF=
,CF= ![]() =
= ![]() ,
,
∵ME=CF,∴![]() ,解得:
,解得:![]() (舍),
(舍),![]() ,
,
故的点M的坐标 为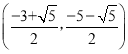 ;
;
④如图4,作ME⊥对称轴,垂足为E,ME交NC,交点为F.
设点M的坐标为(![]() ,
,![]() ),则ME=
),则ME= ![]() ,CF=
,CF= ![]() ,
,
由①同理可证△MNE≌△CFM,
∵ME=CF,故![]() ,
,
解得:![]() ,
,![]() (舍),
(舍),
故点M的坐标为(![]() ,
,![]() );
);
综上可得点M的坐标为: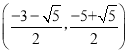 或
或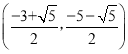 或(
或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).

【题目】某宾馆有若干间标准房,当标准房的价格为200元时,每天入住的房间数为60间,经市场调查表明,该宾馆每间标准房的价格在170~240元之间(含170元,240元)浮动时,每天入住的房间数![]() (间)与每间标准房的价格
(间)与每间标准房的价格![]() (元)的数据如下表:
(元)的数据如下表:
| … | 190 | 200 | 210 | 220 | … |
| … | 65 | 60 | 55 | 50 | … |
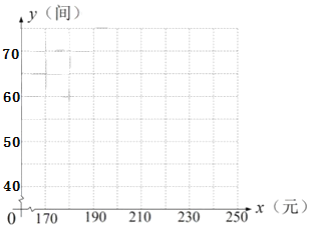
(1)根据所给数据在坐标系中描出相应的点,并画出图象.
(2)求![]() 关于
关于![]() 的函数表达式、并写出自变量
的函数表达式、并写出自变量![]() 的取值范围.
的取值范围.
(3)设客房的日营业额为![]() (元).若不考虑其他因素,问宾馆标准房的价格定为多少元时.客房的日营业额最大?最大为多少元?
(元).若不考虑其他因素,问宾馆标准房的价格定为多少元时.客房的日营业额最大?最大为多少元?