题目内容
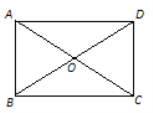
【题目】如图，已知AB 
，在AB，CD之间取一点E，连接EA，EC，试探索
AEC与 EAB， ECD之间的关系
若点E取在AC上
如图
，则 AEC
，由此可得 AEC
EAB
ECD或 AEC EAB ECD
如果点E取在AC的两侧如图
，结论会是什么？
【答案】图②，
AEC
EAB
ECD;图③， AEC EAB ECD
【解析】试题分析：如图②，过点E作EF∥AB，交AC于点F，由AB∥CD，可得AB∥EF∥CD，根据两直线平行，内错角相等，可得∠AEC=∠EAB+∠ECD；如图③，过点E作EF∥AB，交AC于点F，由AB∥CD，可得AB∥EF∥CD，根据两直线平行，同旁内角互补，即可证得∠EAB+∠ECD+∠AEC=360°．
试题解析：
如图②，过点E作EF∥AB，交AC于点F，
∵AB∥CD，
∴AB∥EF∥CD，
∴∠EAB=∠AEF，∠ECD=∠FEC，
∴∠AEC=∠EAB+∠ECD；
如图③，过点E作EF∥AB，交AC于点F，
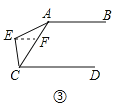
∵AB∥CD，
∴AB∥EF∥CD，
∴∠EAB+∠AEF=180°，∠ECD+∠CEF=180°，
∴∠EAB+∠ECD+∠AEC=360°．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案【题目】泉州市某校准备组织教师、学生、家长到福州进行参观学习活动，旅行社代办购买动车票，动车票价格如下表所示：
运行区间 | 大人票价 | 学生票 | ||
出发站 | 终点站 | 一等座 | 二等座 | 二等座 |
泉州 | 福州 | 61.5（元） | 50.5（元） | 38（元） |
根据报名总人数，若所有人员都买一等座的动车票，则共需13530元，若都买二等座动车票（学生全部按表中的“学生票二等座”购买），则共需8860元；已知家长的人数是教师的人数的3倍。
（1）报名参加活动的总人数为___________人；
（2）求参加活动的教师与学生的人数；
（3）如果买到a张成人二等座票，且学生全部按表中的“学生票二等座”购买，其余的买一等座票，但个别家长因临时不参加活动退票，退票人数刚好是所买一等座票数的
，已知退票的是一等座票，退票收取票价10%的退票费，最终买票的总费用为8859.3元，求a的值。
